Teorema de Varignon

El terme teorema de Varignon fa referència a dos teoremes diferents demostrats ambdós pel matemàtic francès Pierre Varignon (1654-1722), un Teorema matemàtic i un Teorema mecànic.

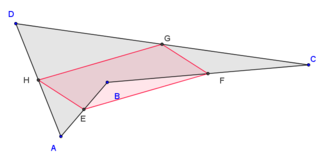
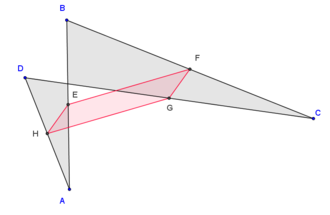
ABCD és un quadrilàter qualsevol, I, J, K i L els punts mitjans dels seus costats. IJKL és un paral·lelogram.

Enunciat: si ABCD és pla i convex, la seva àrea és el doble de IJKL.^[1]

Corol·lari: les mitjanes d'un quadrilàter tenen el mateix punt mitjà (i són les diagonals del paral·lelogram), el perímetre del paral·lelogram de Varignon és igual a la suma de les longituds de les diagonals del quadrilàter.

Aplicant el teorema dels punts mitjans, es mostra que els costats oposats d'IJKL són cadascun paral·lel a una diagonal d'ABCD, per tant, paral·lels entre si.

D'acord amb el teorema de Tales la base b de IJKL és igual a la meitat de la diagonal d d'ABCD, i l'altura h és igual a la meitat de l'altura h'. Agafant-ho d'una punta a l'altre d'ABCD (perpendicularment a la diagonal).

Així:

Àrea (ABCD) = ${\displaystyle {\frac {1}{2}}}$ × d × h’ = ${\displaystyle {\frac {1}{2}}}$ × 2b × 2h = 2 × Àrea (IJKL)

El teorema de Varignon és un teorema descobert per primera vegada pel matemàtic neerlandès Simon Stevin a començaments del segle xvii, però que deu la seva actual forma al matemàtic francès Pierre Varignon (1654-1722), que el va enunciar el 1724 al seu tractat Nouvelle mécanique, com a resultat d'un estudi geomètric en el qual, en contra de l'opinió dels matemàtics francesos de la seva època, va decidir traslladar les idees exposades per Newton a la notació i a l'enfocament que sostenia Leibniz sobre l'anàlisi.

El teorema de Varignon és ara vist, gràcies a l'ús del càlcul vectorial, com una obvietat. Tanmateix, en la seva època va tenir una rellevància fonamental, ja que les forces no eren vistes com a vectors amb un mòdul, direcció i sentits donats, sinó com entelèquies molt abstractes el tractament de les quals es veia complicat a causa d'una semàntica difícil i ineficaç i simbologia (que la notació de Leibniz va resoldre), i per l'ús de tècniques geomètriques molt enginyoses però difícils de tractar.

El seu enunciat, segons la terminologia actual, seria:

Sigui un sistema de n forces concurrents, ${\displaystyle F1,F2...,Fi...,Fn}$, vectors en un espai euclidià, que té com a punt d'aplicació un cert punt A. El moment de cada força ${\displaystyle Fi}$ respecte a ${\displaystyle O}$ serà: ${\displaystyle Mi=rxFi}$ (producte vectorial). Cal notar que escrivim ${\displaystyle r}$ i no ${\displaystyle ri}$, ja que totes les forces s'apliquen en el mateix punt. El moment de la resultant ${\displaystyle R}$ és: ${\displaystyle M=rxR}$ on ${\displaystyle R=F1+F2+Fi+...+Fn}$ i ${\displaystyle r}$ és novament el vector posició comú. Aplicant la propietat del producte vectorial, tenim ${\displaystyle rxR=rx(F1+F2+Fi+...+Fn)}$ ${\displaystyle rxR=rxF1+rxF2+rxFi+...+rxFn)}$ llavors ${\displaystyle M=M1+M2+Mi+...+Mn}$

Després, efectivament "el moment resultant és igual a la suma vectorial dels moments de les forces aplicades si aquestes són concurrents".