Born-Koordinaten

Die Born-Koordinaten beschreiben in der relativistischen Physik eine Karte für einen Teil des flachen Minkowski-Raumes der speziellen Relativitätstheorie, den räumlichen Zylinder mit ${\displaystyle r<1/\omega .}$ Das entsprechende Linienelement mit der Signatur ${\displaystyle (1,3)}$, also ${\displaystyle (+,-,-,-),}$ den natürlichen Einheiten ${\displaystyle G=c=1}$ und der Winkelgeschwindigkeit ${\displaystyle \omega }$ ist

${\displaystyle \mathrm {d} s^{2}=\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}-2\,\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t{,}\,z<\infty {,}\quad 0<r<1/\omega {,}\quad -\pi \leq \phi <\pi .}$

Die Born-Koordinaten werden für die mathematische Analyse der Physik von sogenannten Langevin-Beobachtern benutzt, die auf einem Ring mit konstantem Abstand zum Drehmittelpunkt rotierender starrer Scheiben ruhen (siehe Ehrenfestsches Paradoxon^{[H 1]}). Die erstmalige Beschreibung dieser Koordinaten erfolgte im Zusammenhang mit Max Borns (1909) relativistischer Physik der starren Körper,^{[H 2][H 3]} die für rotierende Körper unter anderem von Gustav Herglotz (1909) weiterentwickelt wurde.^{[M 1]} Für einen allgemeinen Überblick zu Beschleunigungen in der Minkowski-Raumzeit, siehe Beschleunigung (Spezielle Relativitätstheorie).

Ideale ruhende Uhren auf der rotierenden Scheibe lassen sich nicht widerspruchsfrei synchronisieren. Nicht auf einem Ring mit konstantem Durchmesser auf dem die Uhren zumindest gleich schnell laufen, schon gar nicht auf der ganzen Scheibe, auf der die Uhren, je weiter sie von der Drehachse entfernt sind, um den Faktor ${\displaystyle \gamma ^{-1}=(1-\omega {^{2}}r{^{2}})}$ langsamer laufen (Zeitdilatation). Das heißt, dass die Uhren entlang eines Radius mit ${\displaystyle t=\phi =z={\rm {const.}}}$ nicht gleich schnell laufen, sondern im Vergleich mit einer Referenzuhr im Drehmittelpunkt ${\displaystyle r=0}$ mit wachsendem ${\displaystyle r>0}$ langsamer werden.

Da die Born-Koordinaten einen Teil des flachen Minkowski-Raums beschreiben, lassen sich die Uhren wie dort synchronisieren, indem die Uhr im Drehmittelpunkt (Uhr ${\displaystyle {\rm {O}}}$ im Rotationszentrum) als Referenz dient und z. B. im Sekundentakt ein Lichtsignal aussendet, mit dem alle Uhren auf der rotierenden Scheibe synchronisiert werden (siehe Abb. 2). Die Empfängeruhren ${\displaystyle {\rm {L}}}$, ${\displaystyle {\rm {A}}}$ und ${\displaystyle {\rm {B}}}$ kennen die jeweilige Laufzeit des Signals vom Drehmittelpunkt und justieren ihre Uhrzeit entsprechend. Das heißt, dass alle Beobachter, die sich auf der Drehachse befinden, Lichtsignale, die von den Uhren auf der Scheibe im Sekundentakt abgesendet werden, im Sekundentakt empfangen werden. Werden die Signale von Uhren auf einem Ring mit konstantem Radius gesendet, werden sie darüber hinaus gleichzeitig empfangen. Solcherart synchronisiert, sind die Uhren in ${\displaystyle {\rm {A}}}$, ${\displaystyle {\rm {B}}}$, ${\displaystyle {\rm {L}}}$ und ${\displaystyle {\rm {O}}}$ synchron mit der Koordinatenzeit ${\displaystyle t}$ des Inertialsystems, in dem die Drehachse der rotierenden Scheibe ruht.^{[A 1]}

Für den Langevin-Beobachter (Uhr ${\displaystyle {\rm {L}}}$) ist die Situation jedoch nicht zufriedenstellend. Für ihn ergeben sich zwei Probleme. Erstens läuft seine so synchronisierte Uhr zu schnell im Vergleich zu einer Uhr, die er auf die Standard-SI-Sekunde geeicht hat. Zweitens macht er die irritierende Feststellung, dass zwei Lichtsignale, die von den beiden gleich weit entfernten Uhren ${\displaystyle {\rm {A}}}$ und ${\displaystyle {\rm {B}}}$ auf seinem Ring gleichzeitig ausgesendet werden, nicht gleichzeitig bei ihm eintreffen. Da er weiß, dass die Uhren ${\displaystyle {\rm {A}}}$ und ${\displaystyle {\rm {B}}}$ gleich weit von seiner Uhr ${\displaystyle {\rm {L}}}$ entfernt sind, gibt es nur zwei Möglichkeiten. Entweder ist die Lichtausbreitung nicht isotrop – Licht von ${\displaystyle {\rm {A}}}$ in Drehrichtung ist früher bei ihm (die Geschwindigkeit des Lichts wäre daher schneller als ${\displaystyle c}$), als Licht von ${\displaystyle {\rm {B}}}$ entgegen der Drehrichtung (die Geschwindigkeit des Lichts wäre daher langsamer als ${\displaystyle c}$). Oder die Uhren ${\displaystyle {\rm {A}}}$ und ${\displaystyle {\rm {B}}}$ sind mit seiner Uhr ${\displaystyle {\rm {L}}}$ nicht synchron.

Um sie aus seiner Sicht zu synchronisieren geht er wie im Inertialsystem vor. Er eicht die Uhren in ${\displaystyle {\rm {A}}}$, ${\displaystyle {\rm {B}}}$ und ${\displaystyle {\rm {L}}}$ auf die SI-Sekunde und synchronisiert die Uhren ${\displaystyle {\rm {A}}}$ und ${\displaystyle {\rm {B}}}$ mit seiner Uhr ${\displaystyle {\rm {L}}}$ mittels Einstein-Synchronisation (eine interne Synchronisation). Er stellt fest, dass er die Uhr ${\displaystyle {\rm {A}}}$, die in Drehrichtung liegt, zurückstellen muss und die Uhr ${\displaystyle {\rm {B}}}$, die entgegen der Drehrichtung liegt, vorstellen muss. Zwei Lichtsignale, die jetzt gleichzeitig von ${\displaystyle {\rm {A}}}$ und ${\displaystyle {\rm {B}}}$ ausgesendet werden, treffen gleichzeitig bei ${\displaystyle {\rm {L}}}$ ein (sie treffen aber nicht gleichzeitig bei der Uhr ${\displaystyle {\rm {O}}}$ ein). Synchronisiert man alle Uhren entlang des Ringes auf diese Art und Weise, ergibt sich neuerlich ein Problem. Zumindest zwei benachbarte Uhren zeigen nicht die gleiche Zeit. In Summe weisen die Uhren entlang des Rings mit dem Radius r eine Zeitdifferenz ${\displaystyle \Delta t=(2\pi \omega r^{2})/(1-\omega ^{2}r^{2})}$ auf.

Außerdem stellt der Langevin-Beobachter fest, dass, egal wie er die Distanzen seiner lokalen Umgebung vermisst, die Geometrie nicht-euklidisch ist und am besten durch eine Riemannsche Metrik, die sogenannte Langevin-Landau-Lifschitz Metrik beschrieben wird. Diese Metrik wiederum wird sehr gut durch die Metrik der hyperbolischen Ebene angenähert. Bei der Vermessung großer Distanzen über die lokale Umgebung hinaus hängen die Ergebnisse von der Messmethode ab, die sich nicht mit den Eigenschaften einer Riemann Metrik beschreiben lassen. Die mit der Radarmethode gemessenen großen Distanzen sind nicht einmal symmetrisch. Die gemessene Entfernung von ${\displaystyle {\rm {L}}}$ nach ${\displaystyle {\rm {O}}}$ ist nicht gleich der gemessenen Entfernung von ${\displaystyle {\rm {O}}}$ nach ${\displaystyle {\rm {L}}}$. Das heißt, dass die Geometrie der rotierenden Scheibe weder eine euklidische noch eine riemannsche Geometrie ist.

Die rotierende Scheibe ist kein Paradoxon. Egal welche Methode der Langevin-Beobachter verwendet um seine lokale Umgebung zu analysieren: er stellt fest, dass er sich in einem rotierenden Bezugssystem befindet und nicht in einem Inertialsystem.

Für die Herleitung der Born-Koordinaten ist es sinnvoll, die Langevin-Beobachter zuerst in Zylinderkoordinaten darzustellen. Ihre Weltlinien bilden eine zeitartige Kongruenz, die als starr angesehen werden kann, da der entsprechende Expansionstensor verschwindet (siehe unten). Die Langevin-Beobachter rotieren um die Symmetrieachse des Zylinders.

Aus dem Linienelement des Minkowskiraumes in Zylinderkoordinaten

${\displaystyle {\begin{aligned}&\mathrm {d} s^{2}=\mathrm {d} T^{2}-\mathrm {d} Z^{2}-\mathrm {d} R^{2}-R^{2}\,\mathrm {d} \Phi ^{2},\;\;\\&-\infty <T,\;Z<\infty ,\quad 0<R<\infty ,\quad -\pi \leq \Phi <\pi ,\end{aligned}}}$

können unmittelbar die Tetraden (Vektorfelder der Basisvektoren) des lokalen Bezugssystems für stationäre Beobachter abgelesen werden:

${\displaystyle {\vec {e}}_{0}=\partial _{T},\;\;{\vec {e}}_{1}=\partial _{Z},\;\;{\vec {e}}_{2}=\partial _{R},\;\;{\vec {e}}_{3}={\frac {1}{R}}\,\partial _{\Phi }.}$

${\displaystyle {\vec {e}}_{0}}$ ist ein zeitartiges Vektorfeld. ${\displaystyle {\vec {e}}_{1}}$, ${\displaystyle {\vec {e}}_{2}}$ und ${\displaystyle {\vec {e}}_{3}}$ sind raumartige Vektorfelder.

Mit einem Lorentz-Boost der Vektorfelder der Basisvektoren mit ${\displaystyle \omega R}$ in Richtung ${\displaystyle {\vec {e}}_{3}}$ (Anwendung der Lorentz-Transformation auf ${\displaystyle {\vec {e}}_{3}}$ und ${\displaystyle {\vec {e}}_{0}}$) ergeben sich die Vektorfelder der Basisvektoren für die Langevin-Beobachter mit

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\partial _{\Phi },}$

${\displaystyle {\vec {p}}_{1}=\partial _{Z},\;\;{\vec {p}}_{2}=\partial _{R},}$

${\displaystyle {\vec {p}}_{3}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\,\partial _{\Phi }+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}.}$

Diese Vektorfelder wurden erstmals (implizit) von Paul Langevin 1935 verwendet.^{[H 4]} Eine ausführliche Beschreibung erfolgte durch Thomas A. Weber erst 1997.^{[M 2][M 3][M 4]} Definiert sind diese Vektorfelder im Gegensatz zu den Zylinderkoordinaten mit ${\displaystyle 0<R<\infty }$ im Bereich ${\displaystyle 0<R<1/\omega }$. Diese Einschränkung ist fundamental, da sich die Geschwindigkeit der Langevin-Beobachter nahe der Grenze ${\displaystyle R\rightarrow 1/\omega }$ der Lichtgeschwindigkeit nähert.

Jede integrale Kurve des zeitartigen Vektorfeldes ${\displaystyle {\vec {p}}_{0}}$ wird in Zylinderkoordinaten als wendelförmige Kurve mit konstantem Radius abgebildet (siehe die rote Kurven in Abb. 1 und Abb. 3) und repräsentiert einen in Bezug auf die rotierende Scheibe ruhenden Langevin-Beobachter. Weitere Langevin-Beobachter, die sich mit dem ersten auf einem Ring mit dem Radius ${\displaystyle R}$ und der Winkelgeschwindigkeit ${\displaystyle \omega }$ befinden, sollten auf der integralen Kurve des Vektorfeldes ${\displaystyle {\vec {p}}_{3}}$ (siehe die blaue Kurve in Abb. 3) gleichzeitig (synchron) sein. Jedoch zeigt sich, dass sich ideale Uhren entlang der blauen Kurve mittels Einstein-Synchronisation nicht synchronisieren lassen, da sich die blaue Kurve an unterschiedlichen Stellen mit der roten Kurve schneidet. Zumindest zwei benachbarte Uhren zeigen unterschiedliche Zeiten, da die blaue Kurve gleichzeitig ist, zwei unterschiedliche Stellen auf der roten Kurve aber einen zeitlichen Abstand haben – die blaue Kurve ist keine geschlossene Kurve in der Raumzeit und die benachbarten Uhren sie sind nicht synchron. Das ist der erste Hinweis darauf, dass sich für die rotierende Scheibe keine zufriedenstellende Beschreibung einer räumlichen Geometrie finden lässt, auf der alle Ereignisse gleichzeitig sind. Weder für die ganze rotierende Scheibe, noch für einen rotierenden Ring mit Radius ${\displaystyle R}$.

Im Gegensatz dazu, ist die Projektion der wendelförmigen Weltlinie eines Langevin-Beobachters auf die räumliche Hyperebene ${\displaystyle T=\mathrm {const.} }$ ein Kreis – also eine geschlossene Kurve in der Raumzeit. Darüber hinaus ist das Vektorfeld der Basisvektoren ${\displaystyle {\vec {e}}_{3}=(1/R)\,\partial _{\Phi }}$ ein raumartiges Killingvektorfeld, dessen integrale Kurven geschlossene Kurven im Raum sind (de-facto Kreise). Sie degenerieren für ${\displaystyle R=0}$ zu Kurven mit der Länge Null. Das entspricht der Vorstellung der zylindrischen Symmetrie und der Vorstellung eines rotierenden Langevin-Beobachters. Diese Vorstellung basierend auf ${\displaystyle T=\mathrm {const.} }$ lässt sich jedoch nicht realisieren, da die idealen Uhren auf dem Ring nicht widerspruchsfrei synchronisiert werden können und damit ${\displaystyle T=\mathrm {const.} }$ (Gleichzeitigkeit) keinen Sinn ergibt, wenn keine eindeutige Synchronisation der Uhren möglich ist.

Die Viererbeschleunigung des zeitartigen Vektorfeldes ${\displaystyle {\vec {p}}_{0}}$ ist

${\displaystyle \nabla _{{\vec {p}}_{0}}{\vec {p}}_{0}={\frac {-\omega ^{2}\,R}{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{2}.}$

Sie zeigt radial zur Drehachse und hängt nur vom konstanten Radius ${\displaystyle R}$ und der konstanten Winkelgeschwindigkeit ${\displaystyle \omega }$ der wendelförmigen Weltlinie des Langevin-Beobachters ab (Zentripetalbeschleunigung). Mit der kinematischen Dekomposition (siehe Viererbeschleunigung oben) ergeben sich der Expansionstensor und der Wirbelvektor.^{[A 2]} Der Expansionstensor ist Null. Das heißt, dass die Abstände der Langevin-Beobachter zueinander und zur Drehachse konstant bleiben (starren Scheibe). Der Wirbelvektor ergibt sich mit

${\displaystyle {\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{1}}$

und ist parallel zur Drehachse. Das heißt, dass die Langevin-Beobachter um die Drehachse rotieren. Das heißt aber auch, dass die Langevin-Beobachter um ihre eigene Achse rotieren. Das entspricht der Vorstellung einer lokalen Verwirbelung. In Abb. 4 zeigt die cyanfarbene Kurve, wie sich die raumartigen Vektorfelder ${\displaystyle {\vec {p}}_{2},\;{\vec {p}}_{3}}$ um das Vektorfeld ${\displaystyle {\vec {p}}_{1}}$ winden (${\displaystyle {\vec {p}}_{1}}$ – die ${\displaystyle Z}$-Koordinate – ist in der Abb. 4 durch ${\displaystyle {\vec {e}}_{0}}$ – die Zeit – ersetzt, da die ${\displaystyle Z}$-Koordinate hier keine Rolle spielt). Die lokalen Bezugssysteme der Langevin-Beobachter rotieren also auch und sind keine Inertialsysteme und ihre ${\displaystyle {\vec {p}}_{2}=\partial _{R}}$ sind mit dem radial Basisvektor ${\displaystyle {\vec {e}}_{2}=\partial _{R}}$ ausgerichtet. Diese lokale Rotation von ${\displaystyle {\vec {p}}_{2}}$ und ${\displaystyle {\vec {p}}_{3}}$ um die Achse ${\displaystyle {\vec {p}}_{1}}$ kann durch eine konstante lokale Gegenrotation aufgehoben werden.

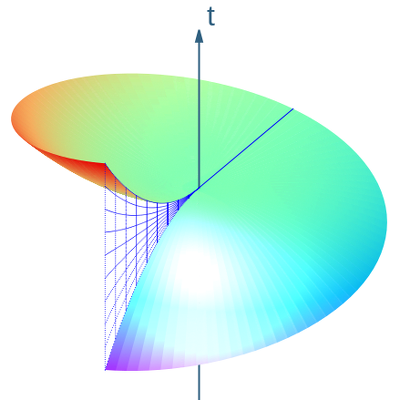
Um die Born-Koordinaten zu erhalten, werden die wendelförmigen Weltlinien der Langevin-Beobachter mittels der Transformation

${\displaystyle t=T,\;\;z=Z,\;\;r=R,\;\;\phi =\Phi -\omega \,T}$

„gestreckt“ und es ergibt sich das neue Linienelement

${\displaystyle \mathrm {d} s^{2}=\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}-2\,\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t,\,z<\infty ,\quad 0<r<{\frac {1}{\omega }},\quad -\pi <\phi <\pi .}$

Wegen des Mischterms ${\displaystyle \omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi }$ sind die Born-Koordinaten kein orthogonales Koordinatensystem.

Die Weltlinien der Langevin-Beobachter sind jetzt gerade vertikale Linien. In Born-Koordinaten sind die Vektorfelder der Basisvektoren der Langevin-Beobachter

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t},}$

${\displaystyle {\vec {p}}_{1}=\partial _{z},\;\;{\vec {p}}_{2}=\partial _{r},}$

${\displaystyle {\vec {p}}_{3}={\frac {\sqrt {1-\omega ^{2}\,r^{2}}}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}.}$

Die wendelförmigen Weltlinien der Langevin-Beobachter in Zylinderkoordinaten sind in Born-Koordinaten gerade Linien. Jedoch sind die geraden Weltlinien der statischen Beobachter in Zylinderkoordinaten, die neben der rotierenden Scheibe ruhen, in Born-Koordinaten wendelförmige Weltlinien. Im Gegensatz zu den Zylinderkoordinaten, sind nicht nur die Vektorfelder der Basisvektoren der Langevin-Beobachter auf den Bereich ${\displaystyle 0<r<1/\omega }$ beschränkt, sondern die Born-Koordinaten insgesamt.

Die kinematische Dekomposition der zeitartigen Kongruenz ${\displaystyle \textstyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$ liefert die gleichen Ergebnisse wie zuvor, jedoch mit den neuen Born-Koordinaten. Der Beschleunigungsvektor ist

${\displaystyle \nabla _{{\vec {p}}_{0}}\,{\vec {p}}_{0}={\frac {-\omega ^{2}\,r}{1-\omega ^{2}\,r^{2}}}\,{\vec {p}}_{2},}$

der Expansionstensor ist Null und der Wirbelvektor ist

${\displaystyle {\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,r^{2}}}\;{\vec {p}}_{1}.}$

Das zu einem zeitartigen Einheitsvektorfeld duale Kovektorfeld definiert in jedem lokalen Bezugssystem eine infinitesimale räumliche Hyperebene. Ob diese infinitesimalen räumlichen Hyperebenen zu einer globalen räumlichen Hyperebene verbunden werden können, die überall zur Kongruenz der Weltlinien orthogonal ist, wird durch die Bedingung für die vollständige Integrierbarkeit bestimmt. Es zeigt sich, dass diese Bedingung genau dann und nur dann erfüllt ist, wenn der Wirbeltensor Null ist. Für den statischen Beobachter in Zylinderkoordinaten existieren solche räumliche Hyperflächen für die ${\displaystyle T=\mathrm {const.} }$ gilt, für den Langevin-Beobachter jedoch nicht. Insbesondere sind die räumlichen Hyperflächen ${\displaystyle t=\mathrm {const.} }$ in Born-Koordinaten orthogonal zu den Weltlinien der statischen Beobachter, nicht zu den Weltlinien der Langevin-Beobachter.

Dies wird deutlich, wenn die Integralkurven des Langevin-Vektorfeldes

${\displaystyle {\vec {p}}_{3}={\sqrt {1-\omega ^{2}\,r^{2}}}\,{\frac {1}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t},}$

die durch den Radius ${\displaystyle \phi =0,\,t=0}$ verlaufen, dargestellt werden. Diese Kurven liegen in der Fläche

${\displaystyle \phi +\omega \,t-{\frac {t}{\omega \,r^{2}}}=0,\;\;-\pi <\phi <\pi }$

(siehe Abb. 5). Die für die Darstellung unwesentliche Koordinate ${\displaystyle z}$ wurde durch die Koordinate ${\displaystyle t}$ ersetzt. Es liegt nahe, diese Fläche als räumliche „Gleichzeitigkeitsfläche“ für Langevin-Beobachter zu interpretieren. Dies ist aus zwei Gründen nicht möglich. Erstens ist die Bedingung für die vollständige Integrierbarkeit nicht erfüllt, sodass es keine räumliche Hyperfläche gibt zu der die Vektorfelder ${\displaystyle {\vec {p}}_{2},\,{\vec {p}}_{3}}$ tangential sind. Das Vektorfeld ${\displaystyle {\vec {p}}_{2}}$ ist nur für ${\displaystyle \phi =0}$ tangential. Das ist ein infinitesimales (lokales) Problem. Zweitens wird in Abb. 5 ersichtlich, dass die so konstruierte räumliche Hyperebene eine Unstetigkeit aufweist, einen Sprung (siehe die blauen Gitterlinien Abb. 5). Das ist ein globales Problem und eine Konsequenz daraus, dass sich die Uhren der Langevin-Beobachter nicht widerspruchsfrei synchronisieren lassen. Weder auf der ganzen rotierenden Scheibe, noch auf einem Ring mit konstantem ${\displaystyle r}$.

Die Nullgeodäten in Zylinderkoordinaten ergeben sich aus den Geodätengleichungen^{[A 3]}

${\displaystyle {\ddot {T}}=0,\;\;{\ddot {Z}}=0,\;\;{\ddot {R}}-R\,{\dot {\Phi }}^{2}=0,\;\;{\ddot {\Phi }}+{\frac {2}{R}}\,{\dot {\Phi }}\,{\dot {R}}=0.}$

Die ersten Integrale für ${\displaystyle {\ddot {T}},\,{\ddot {Z}},\,{\ddot {\Phi }}}$ lassen sich unmittelbar angeben mit

${\displaystyle {\dot {T}}=E,\;\;{\dot {Z}}=P,\;\;{\dot {\Phi }}={\frac {L}{R^{2}}}.}$

Wird das in den Ausdruck für das Linienelement der Zylinderkoordinaten eingesetzt und wird außerdem ${\displaystyle \mathrm {d} s^{2}=0}$ (für die Nullgeodäte) gesetzt, so ergibt sich

${\displaystyle {\dot {R}}^{2}=E^{2}-P^{2}-{\frac {L^{2}}{R^{2}}}\geq 0.}$

Daraus ergibt sich für den minimalen Radius R_min einer Nullgeodäte

${\displaystyle E^{2}-P^{2}-{\frac {L^{2}}{R_{\mathrm {min} }^{2}}}=0\quad }$ also ${\displaystyle \quad R_{\mathrm {min} }={\frac {|L|}{\sqrt {E^{2}-P^{2}}}}}$

und weiter

${\displaystyle {\dot {R}}^{2}=L^{2}\left({\frac {1}{R_{\mathrm {min} }^{2}}}-{\frac {1}{R^{2}}}\right).}$

Damit ist für ${\displaystyle {\ddot {R}}}$ das erste Integral ebenfalls gefunden.

Die Lösung der Nullgeodäten als Kurven mit dem affinen Parameter λ ist (siehe Abb. 6)

${\displaystyle {\begin{aligned}R&={\sqrt {(E^{2}-P^{2})\,\lambda ^{2}+L^{2}/(E^{2}-P^{2})}}=\\&={\sqrt {(E^{2}-P^{2})\,\lambda ^{2}+R_{\mathrm {min} }^{2}}},\\T&=T_{0}+E\,\lambda ,\\[1em]Z&=Z_{0}+P\,\lambda ,\\\Phi &=\Phi _{0}+\operatorname {arctan} \left({\frac {E^{2}-P^{2}}{L}}\,\lambda \right)=\\&=\Phi _{0}+\operatorname {arctan} \left({\frac {\sqrt {E^{2}-P^{2}}}{R_{\mathrm {min} }\,\operatorname {sgn} {(L)}}}\,\lambda \right).\end{aligned}}}$

Die Trajektorien der Nullgeodäten, also die Spuren ihrer „Projektion“ in die räumliche Hyperebene ${\displaystyle T=\mathrm {const.} }$ sind im Minkowski-Raum mit Zylinderkoordinaten natürlich Geraden und gegeben durch

${\displaystyle R={\frac {R_{\mathrm {min} }}{\cos(\Phi -\Phi _{0})}}.}$

Für radiale Nullgeodäten ist ${\displaystyle R_{\mathrm {min} }=0}$. Außerdem gilt mit ${\displaystyle E=1,\,P=0}$ in die Gleichungen oben eingesetzt für auslaufende radiale Nullgeodäten

${\displaystyle T=\lambda ,\;Z=Z_{0},\;R=\lambda ,}$

${\displaystyle \Phi =\mathrm {const.} =\omega \,R_{0}.}$

${\displaystyle R_{0}}$ ist der Abstand des Langevin-Beobachters vom Rotationszentrum (siehe Abb. 7). Werden diese Gleichungen in Born-Koordinaten transformiert, ergibt sich für den auslaufenden Lichtstrahl

${\displaystyle r=r_{0}-{\frac {\phi }{\omega }}.}$

In Born-Koordinaten ist diese Trajektorie keine Gerade (siehe die grüne Kurve in der Abb. 7). Wie im Abschnitt Transformation in Born-Koordinaten gezeigt, handelt es sich in Born-Koordinaten bei diesen Trajektorien streng genommen nicht um eine Projektion in eine räumliche Hyperebene, da eine solche für ${\displaystyle t=\mathrm {const.} }$ nicht definiert ist (siehe Abb. 5).

Für einlaufende radiale Nullgeodäten ergibt sich

${\displaystyle r={\frac {\phi }{\omega }}}$

dargestellt als rote Kurve in Abb. 7.

Um einen Laserimpuls zum stationären Beobachter S bei r = 0 zu senden, muss der Langevine-Beobachter bei r = R₀ voraus zielen (für ihn bewegt sich S gegen den Uhrzeigersinn von rechts nach links). Das Gleiche gilt für den Beobachter S, der einen Laserimpuls zum Beobachter L schicken will. Für ω > 0 sind die ein- und auslaufenden Nullgeodäten unterschiedliche Kurven in der Raumzeit mit unterschiedlichen Trajektorien.

Nullgeodäten zwischen Langevin-Beobachtern auf dem Ring mit r = R₀ sind für ω > 0 ebenfalls nach innen oder nach außen gebogen. Um dies zu sehen, werden die Gleichungen für die in Rotationsrichtung laufenden Nullgeodäten in Zylinderkoordinaten in der Form

${\displaystyle T=R_{\mathrm {min} }\,\tan(\Phi ),}$

${\displaystyle R={\frac {R_{\mathrm {min} }}{\cos(\Phi )}}}$

geschrieben. Die Transformation in Born-Koordinaten ergibt

${\displaystyle t=r_{\mathrm {min} }\,\tan(\phi +\omega \,t),}$

${\displaystyle r={\frac {r_{\mathrm {min} }}{\cos(\phi +\omega \,t)}}}$

oder nach r und ϕ aufgelöst

${\displaystyle r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},}$

${\displaystyle \phi =-\omega \,t+\operatorname {arctan} (t/r_{\mathrm {min} }).}$

Diese Trajektorie ist für ω > 0 tatsächlich nach innen gebogen (siehe die grüne Kurve in Abb. 7). Für Nullgeodäten gegen die Rotationsrichtung (siehe die rote Kurve in Abb. 7) ergeben sich die Kurven

${\displaystyle r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},}$

${\displaystyle \phi =-\omega \,t-\operatorname {arctan} (t/r_{\mathrm {min} })}$

deren Trajektorien nach außen gebogen sind. Für die Langevin-Beobachter gilt, dass sie um sich Laserimpulse zu senden vorhalten müssen.

Damit sind die Betrachtungen zu Nullgeodäten abgeschlossen, denn eine Nullgeodäte ist entweder radial oder hat einen minimalen Radius r_min.

Für beschleunigte Beobachter gibt es selbst im einfachsten Fall des flachen Minkowski-Raumes verschiedene Möglichkeiten zur Entfernungsmessung, die sich als operational sinnvoll erweisen. Von diesen ist die Radardistanz die einfachste. Misst ein stationärer Beobachter C im Drehzentrum der Scheibe R = r = 0 die Laufzeit zu einem Langevin-Beobachter A auf einem Ring mit dem Radius ${\displaystyle r_{0}}$, so erhält er als Ergebnis ${\displaystyle r_{0}}$. Für den Langevin-Beobachter A ist die Situation anders. Er misst eine etwas kürzere Laufzeit, da seine Uhr im Vergleich zur Uhr des stationären Beobachters C um den Faktor ${\displaystyle {\sqrt {1-\omega ^{2}r_{0}^{2}}}}$ zeitdilatiert ist. Er erhält als Ergebnis seiner Messung ${\displaystyle r_{0}{\sqrt {1-\omega ^{2}r_{0}^{2}}}}$. Bereits dieser einfache Fall zeigt sich widersprüchlich. Die Beobachter A und C sind sich über ihren Abstand nicht einig. Die Radarmessung liefert kein symmetrisches Ergebnis.

Im Vergleich dazu liefert die Radarmessung zwischen zwei Langevin-Beobachtern A und B auf dem Ring mit dem Radius ${\displaystyle r_{0}}$ ein symmetrisches Ergebnis. Der Beobachter A misst den Abstand zu B gleich wie der Beobachter B den Abstand zu A (siehe Abb. 9). Die Laufzeiten zwischen A und B können mit den Gleichungen für die allgemeinen Nullgeodäten ermittelt werden. Mit dem Winkel ΔΦ zwischen A und B ergibt sich für die Laufzeit Δt_AB (in Koordinatenzeit) von A nach B

${\displaystyle \Delta \phi =+\omega \,\Delta t_{AB}+2\operatorname {arctan} \left(\Delta t_{AB}/{\sqrt {4r_{0}^{2}-\Delta t_{AB}^{2}}}\right)}$

und für die Laufzeit Δt_BA (in Koordinatenzeit) von B nach A

${\displaystyle \Delta \phi =-\omega \,\Delta t_{BA}+2\operatorname {arctan} \left(\Delta t_{BA}/{\sqrt {4r_{0}^{2}-\Delta t_{BA}^{2}}}\right).}$

Die beiden Laufzeiten können mit diesen nichtlinearen Gleichungen numerisch berechnet werden. Die Radardistanz unter Berücksichtigung der Zeitdilatation ist damit

${\displaystyle l={\sqrt {1-\omega ^{2}r^{2}}}\;{\frac {\Delta t_{AB}+\Delta t_{BA}}{2}}.}$

Trotz der dargestellten Schwierigkeiten bei der Bestimmung von Radardistanzen im Großen lässt sich beispielsweise mit Märzke-Wheeler-Koordinaten für einen bestimmten Langevin-Beobachter eine Gleichzeitigkeitsfläche konstruieren, mit deren Hilfe sich große Radardistanzen messen lassen.^{[M 5]}

Wie im Abschnitt Transformation in Born-Koordinaten gezeigt, lassen sich mit Born-Koordinaten keine „Gleichzeitigkeitsflächen“ festlegen. Jedoch ist die zeitartige Kongruenz der Langevin-Beobachter stationär und ihre Weltlinien können durch Punkte ersetzt werden. Dadurch wird ein Quotientenraum des Bereichs ${\displaystyle 0<R<1/\omega }$ des Minkowskiraums gebildet. Dieser Raum ist eine dreidimensionale topologische Mannigfaltigkeit, die sich durch eine Riemannsche Metrik in eine dreidimensionale Riemannsche Mannigfaltigkeit wandeln lässt, mit der sich einfach operational Abstände finden lassen.

Ausgangspunkt ist das Linienelement in Born-Koordinaten

${\displaystyle \mathrm {d} s^{2}=(1-\omega ^{2}\,r^{2})\,\mathrm {d} t^{2}-2\,\omega \,r^{2}\,\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\,\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t,z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi .}$

Wird ${\displaystyle \mathrm {d} s^{2}=0}$ gesetzt und nach ${\displaystyle \mathrm {d} t}$ aufgelöst, ergeben sich die Lichtlaufzeiten hin und zurück

${\displaystyle \mathrm {d} t_{+}={\frac {\omega \,r^{2}\,\mathrm {d} \phi +{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle \mathrm {d} t_{-}={\frac {\omega \,r^{2}\,\mathrm {d} \phi -{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}}.}$

Und damit die lokale (infinitesimale) Radardistanz als arithmetischer Mittelwert der Lichtlaufeigenzeit

${\displaystyle {\sqrt {1-\omega ^{2}\,r^{2}}}\;{\frac {\mathrm {d} t_{+}-\mathrm {d} t_{-}}{2}}={\sqrt {\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}}}}.}$

Somit hat der Quotientenraum das Riemannsche Linienelement

${\displaystyle \mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle -\infty <z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi }$

das dem Abstand zweier benachbarter Langevin-Beobachter mit infinitesimalem Abstand entspricht. Diese Metrik wird Langevin-Landau-Lifschitz-Metrik genannt und stellt die „Radardistanz im Kleinen“ dar. Diese Metrik wurde von Langevin eingeführt und von Lifschitz und Landau als „Radardistanz im Kleinen“ für durch beliebige stationäre zeitartige Kongruenzen gebildete Quotientenräumen von Lorentzmannigfaltigkeiten verallgemeinert.

Für den Quotientenraum der Langevin-Landau-Lifschitz-Metrik berechnet sich der Krümmungsskalar mit

${\displaystyle {R}={\frac {-6\omega ^{2}}{(1-\omega ^{2}r^{2})^{2}}}=-6\omega ^{2}+{\mathcal {O}}(\omega ^{4}).}$

Dieser ist bis Größen vierter Ordnung in ${\displaystyle \omega }$ identisch mit der konstanten negativen Krümmung des Hyperbolischen Raums mit dem Linienelement

${\displaystyle \mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {\sinh ^{2}({\sqrt {3}}\omega r)}{3\omega ^{2}}}\;\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <z<\infty ,\;\;0<r<\infty ,\;\;-\pi <\phi <\pi }$

und dem Krümmungsskalar

${\displaystyle {R}=-6\omega ^{2}.}$

In diesem Sinne ist die „Geometrie der rotierenden Scheibe“ tatsächlich gekrümmt und entspricht in der Näherung dem Hyperbolischen Raum, wie Theodor Kaluza bereits 1910 (ohne Beweis) vermutet hat. Wie jedoch oben gezeigt wurde, gibt es unterschiedliche Möglichkeiten Abstände auf der rotierenden Scheibe zu messen, die sehr unterschiedliche Ergebnisse liefern. Mit der Langevin-Landau-Lifschitz-Metrik lässt sich ebenso wie mit der Radardistanz im Großen, der radiale Abstand eines Langevin-Beobachters am Ring mit Radius ${\displaystyle r_{0}}$ vom Rotationszentrum ermitteln. Dazu wird das entsprechende Linienelement für die oben angegebene Nullgeodäte integriert.

${\displaystyle \mathrm {d} r={\frac {\mathrm {d} \phi }{\omega }},\quad \mathrm {d} z=0}$

in das Linienelement eingesetzt ergibt

${\displaystyle \int _{0}^{\Delta }\mathrm {d} \sigma =\int \limits _{0}^{r_{0}}{\left(1+{\frac {\omega ^{2}r^{2}}{1-\omega ^{2}r^{2}}}\right)^{\frac {1}{2}}}\,\mathrm {d} r}$

und weiter

${\displaystyle \Delta =\int _{0}^{r_{0}}{\frac {\mathrm {d} r}{\sqrt {1-\omega ^{2}\,r^{2}}}}={\frac {\arcsin(\omega r_{0})}{\omega }}=r_{0}+{\frac {\omega ^{2}\,r_{0}^{3}}{6}}+{\mathcal {O}}(r_{0}^{5}).}$

Dieser Abstand ist größer als ${\displaystyle r_{0}}$, während die „Radardistanz im Großen“ gleich oder kleiner als ${\displaystyle r_{0}}$ ist.

Da die zugrunde liegende Langevin-Landau-Lifschitz-Metrik eine Riemann-Metrik ist, ist dieser Abstand im Gegensatz zur „radialen Radardistanz im Großen“ symmetrisch. Der Riemannsche Krümmungstensor der (gekrümmten) Langevin-Landau-Lifschitz-Metrik ist operational signifikant. Wie Nathan Rosen festgestellt hat, stimmen für benachbarte Langevin-Beobachter die gemessenen lokalen (infinitesimalen) Abständen mit jenen überein, die von einem inertialen Beobachter gemessen werden, der sich in einem bestimmten Augenblick parallel und synchron zu ihnen bewegt.

• Geschichte der speziellen Relativitätstheorie – Starre Körper und Realität der Längenkontraktion
• Paul Ehrenfest
• Nichteuklidische Geometrie
• Laserkreisel
• Tests der speziellen Relativitätstheorie

1. ↑ Ehrenfest, P.: Gleichförmige Rotation starrer Körper und Relativitätstheorie. In: Phys. Zeitschrift. 10. Jahrgang, 1909, S. 918. 
   • Wikisource (englisch): Uniform Rotation of Rigid Bodies and the Theory of Relativity
2. ↑ Born, M.: Die Theorie des starren Elektrons in der Kinematik des Relativitäts-Prinzipes. In: Ann. Phys. 30. Jahrgang, 1909, S. 1, doi:10.1002/andp.19093351102, bibcode:1909AnP...335....1B. 
   • Wikisource (englisch): The Theory of the Rigid Electron in the Kinematics of the Principle of Relativity
3. ↑ Born, M.: Zur Kinematik des starren Körpers im System des Relativitätsprinzips. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. 2. Jahrgang, 1910, PPN252457811, S. 161–179. 
4. ↑ Langevin, P.: Remarques au sujet de la Note de Prunier. In: C. R. Acad. Sci. Paris. 200. Jahrgang, 1935, S. 48. 

1. Grøn, Ø.: Relativistic description of a rotating disk. In: Amer. J. Phys. 43. Jahrgang, Nr. 10, 1975, S. 869–876, doi:10.1119/1.9969, bibcode:1975AmJPh..43..869G. 
2. Landau, L. D., Lifschitz, E. M.: The Classical Theory of Fields (4th ed.). Butterworth-Heinemann, London 1980, ISBN 0-7506-2768-9. 
   • Für die Beschreibung der Langevin-Landau-Litschitz-Metrik als Quotient einer Lorentzschen Mannigfaltigkeit durch eine stationäre Kongruenz siehe Abschnitt 84 und das Beispiel für die Anwendung eines Langevin-Beobachters am Ende des Abschnitts 89.

1. ↑ Siehe den englischen Artikel Born rigidity
2. ↑ Weber, T., A.: A note on rotating coordinates in relativity. In: American Journal of Physics. 65. Jahrgang, Nr. 6, Juni 1997, ISSN 0002-9505, S. 486–487, doi:10.1119/1.18575. 
   • Thomas A. Weber (* 1934) ist emeritierter Professor für theoretische Physik an der Iowa State University. Er erwarb seinen Doktor an der University of Notre Dame 1961. Er befasste sich unter anderem mit mathematischer Physik, Relativitätstheorie und formaler Streutheorie. 1997 beschrieb er als erster ausführlich das Vektorfeld der Basisvektoren für Langevin-Beobachter. Paul Langevin verwendete dieses Vektorfeld als erster 1935 ohne es ausdrücklich zu beschreiben, daher sind die durch dieses Vektorfeld charakterisierten Langevin-Beobachter nach ihm benannt.
3. ↑ Weber, T., A.: Measurements on a rotating frame in relativity, and the Wilson and Wilson experiment. In: American Journal of Physics. 65. Jahrgang, Nr. 10, Oktober 1997, ISSN 0002-9505, S. 946–988, doi:10.1119/1.18696. 
4. ↑ Rizzi, G., Ruggiero, M. L.: Relativity in Rotating Frames: Relativistic Physics in Rotating Reference Frames. Springer-Science+Business Media Dordrecht, Dordrecht 2004, ISBN 978-90-481-6514-8, doi:10.1007/978-94-017-0528-8. 
   • Bietet einen historischen Überblick zum Ehrenfest-Paradoxon von Øyvind Grøn, Beiträge von Neil Ashby, Thomas A. Weber und anderen Autoren, eine Diskussion der Langevin-Kongruenz von Lluís Bel und zahlreiche weitere Referenzen zum Thema.
5. ↑ Pauri, M., Vallisneri, M.: Märzke-Wheeler coordinates for accelerated observers in special relativity. In: Found. Phys. Lett. 13. Jahrgang, Nr. 5, 2000, S. 401–425, doi:10.1023/A:1007861914639. 
   • Konstruktion eines Koordinatensystems für einen Langenvin-Beobachter mittels Radarmessung für große Distanzen (siehe auch die Eprint-Version).

1. ↑ Dabei handelt es sich um eine externe Synchronisation. Eine Konsequenz dieser Methode ist, dass für die Uhr ${\displaystyle {\rm {O}}}$ im Drehmittelpunkt die Sekunde der Uhren auf der Scheibe identisch ist mit ihrer eigenen Sekunde.
2. ↑ Der Wirbeltensor ist ein schiefsymmetrischer Tensor mit drei Dimensionen, der als dreidimensionaler Vektor (Wirbelvektor) dargestellt werden kann.
3. ↑ Ein Punkt bedeutet die erste Ableitung nach dem affinen Parameter ${\displaystyle \lambda }$, zwei Punkte die zweite Ableitung nach dem affinen Parameter ${\displaystyle \lambda }$.

• The Rigid Rotating Disk in Relativity, by Michael Weiss (1995), from the sci.physics FAQ.
• arxiv:gr-qc/9904078: Hrvoje Nikolic: Relativistic contraction and related effects in noninertial frames.
• arxiv:gr-qc/0207104: Guido Rizzi, Matteo Luca Ruggiero: Space geometry of rotating platforms: an operational approach.
• arxiv:gr-qc/0403111: Olaf Wucknitz: Sagnac effect, twin paradox and space-time topology – Time and length in rotating systems and closed Minkowski space-times.