Einundzwanzigeck

Ein Einundzwanzigeck, auch 21‐Eck oder Ikosihenagon (von altgriechisch εἰκοσιείς eikosieís, deutsch ‚einundzwanzig‘ und γωνία gōnía, deutsch ‚Winkel, Ecke‘),^[1] ist ein Polygon mit 21 Seiten und 21 Ecken.

Das regelmäßige 21‐Eck, bei dem alle Seiten gleich lang sind und alle Eckpunkte gedanklich auf einem gemeinsamen Umkreis liegen, ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel kein konstruierbares Polygon, sodass ein regelmäßiges 21‐Eck allein mit Zirkel und Lineal nicht konstruierbar ist.

Allgemein gilt für die Anzahl ${\displaystyle d(n)}$ der Diagonalen in einem ${\displaystyle n}$‐Eck

${\displaystyle d(n)={\frac {n\left(n-3\right)}{2}},}$

somit besitzt das 21‐Eck 189 Diagonalen. Für jede der 21 Ecken, an der eine Diagonale anfangen kann, gibt es 18 mögliche Endpunkte. Diese Anzahl muss aber noch durch 2 geteilt werden, damit keine Diagonale doppelt gezählt wird.

So ergeben sich die genannten ${\displaystyle {\frac {21\cdot 18}{2}}=189}$ Diagonalen.

Größen eines regelmäßigen 21‐Ecks
Innenwinkel	${\displaystyle {\begin{aligned}\alpha &=180^{\circ }\!-{\frac {360^{\circ }\!}{n}}=180^{\circ }\!-{\frac {360^{\circ }\!}{21}}\\\alpha &=162{,}{\overline {857142}}^{\circ }\end{aligned}}}$
Zentriwinkel (Mittelpunktswinkel)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }\!}{21}}\\\mu &=17{,}{\overline {142857}}^{\circ }\end{aligned}}}$
Seitenlänge	${\displaystyle {\begin{aligned}a&=2R\cdot \sin {\frac {180^{\circ }\!}{21}}\\a&\approx 0{,}298085\cdot R\end{aligned}}}$
Umkreisradius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin {\frac {180^{\circ }\!}{21}}}}\\R&\approx {\frac {a}{0{,}298085}}\approx 3{,}354753\cdot a\end{aligned}}}$
Inkreisradius	${\displaystyle {\begin{aligned}r&=R\cdot \cos {\frac {180^{\circ }\!}{21}}\\r&\approx 0{,}988831\cdot R\end{aligned}}}$
Höhe	${\displaystyle {\begin{aligned}h&=R+r=R\cdot \left(1+\cos {\frac {180^{\circ }\!}{21}}\right)\\h&\approx 1{,}988831\cdot R\end{aligned}}}$
Flächeninhalt	${\displaystyle {\begin{aligned}A&=21\cdot R^{2}\cdot \sin {\frac {180^{\circ }\!}{21}}\cdot \cos {\frac {180^{\circ }\!}{21}}\\A&\approx 3{,}094929\cdot R^{2}\end{aligned}}}$

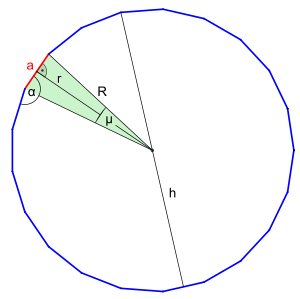
Der Innenwinkel ${\displaystyle \alpha }$ wird von zwei benachbarten Seiten der Länge ${\displaystyle a}$ eingeschlossen.

${\displaystyle \alpha =180^{\circ }\!-{\frac {360^{\circ }}{n}}=180^{\circ }\!-{\frac {360^{\circ }}{21}}=162\;\!\!{\tfrac {6}{7}}^{\circ }}$

Der Zentriwinkel oder Mittelpunktswinkel ${\displaystyle \mu }$ wird von zwei benachbarten Umkreisradien der Länge ${\displaystyle R}$ eingeschlossen.

${\displaystyle \mu ={\frac {360^{\circ }\!}{n}}={\frac {360^{\circ }\!}{21}}=17\!{\tfrac {1}{7}}^{\circ }}$

Die Seitenlänge ${\displaystyle a}$ errechnet sich zu

${\displaystyle a=2R\cdot \sin {\frac {180^{\circ }\!}{21}}}$ .

Der Radius ${\displaystyle R}$ des Umkreises ergibt sich durch Umformen der Formel für die Seitenlänge ${\displaystyle a}$ zu

${\displaystyle R={\frac {a}{2}}\cdot \csc {\frac {180^{\circ }\!}{21}}}$ .

Der Inkreisradius ${\displaystyle r}$ ist die Höhe eines gleichschenkligen Teildreiecks mit den beiden Schenkeln gleich dem Umkreisradius ${\displaystyle R}$ und der Grundlinie gleich der Seitenlänge ${\displaystyle a}$:

${\displaystyle {\begin{aligned}r&=R\cdot \cos {\frac {\mu }{2}}=R\cdot \cos {\frac {180^{\circ }\!}{21}}\end{aligned}}}$

Die Höhe ${\displaystyle h}$ eines regelmäßigen 21‐Ecks ergibt sich aus der Summe von Inkreisradius ${\displaystyle r}$ und Umkreisradius ${\displaystyle R}$:

${\displaystyle h\ =\ R+r\ =\ R+R\cdot \cos {\frac {180^{\circ }\!}{21}}=R\cdot \left(1+\cos {\frac {180^{\circ }\!}{21}}\right)}$

Der Flächeninhalt eines Dreiecks berechnet sich allgemein zu ${\displaystyle A_{\Delta }={\tfrac {1}{2}}a\cdot h_{a}}$. Für die Berechnung des 21‐Ecks werden die Ergebnisse der Seitenlänge ${\displaystyle a}$ und des Inkreisradius ${\displaystyle r}$ herangezogen, worin ${\displaystyle r}$ für die Höhe ${\displaystyle h_{a}}$ eingesetzt wird:

${\displaystyle a=2R\cdot \sin {\frac {180^{\circ }\!}{21}}}$,

${\displaystyle h_{a}=r=R\cdot \cos {\frac {180^{\circ }\!}{21}}}$,  daraus folgt für die Fläche eines Teildreiecks

${\displaystyle A_{\Delta }={\frac {1}{2}}\cdot 2R\cdot \sin {\frac {180^{\circ }\!}{21}}\cdot R\cdot \cos {\frac {180^{\circ }\!}{21}}}$,  zusammengefasst ergibt sich

${\displaystyle A_{\Delta }=R^{2}\cdot \sin {\frac {180^{\circ }\!}{21}}\cdot \cos {\frac {180^{\circ }\!}{21}}}$  und für die Fläche des ganzen 21‐Ecks

${\displaystyle A=21\ A_{\Delta }=21\ R^{2}\cdot \sin {\frac {180^{\circ }\!}{21}}\cdot \cos {\frac {180^{\circ }\!}{21}}}$ .

Ein regelmäßiges 21‐Eck ist, wie im gleichnamigen Absatz begründet, nicht mit Zirkel und Lineal konstruierbar. Verwendet man jedoch ein zusätzliches Hilfsmittel wie z. B. den Tomahawk zur exakten Dreiteilung (Trisektion) eines Winkels oder ein spezielles Kurvenlineal mit der Kurvenform der archimedischen Spirale bzw. der Quadratrix des Hippias für die Teilung des 90-Grad-Winkels in ${\displaystyle n}$ gleich große Winkelweiten, ist eine exakte Lösung machbar.

Um den Tomahawk für die Bestimmung des Zentriwinkels nutzen zu können, bedarf es dafür zuerst einer evtl. komplizierten Konstruktion mindestens einer geeigneten Winkelweite, wie im Beispiel Siebeneck von Andrew M. Gleason zu sehen ist.

Dagegen bietet sowohl die archimedische Spirale als auch die Quadratrix des Hippias einen einfachen und kurzen Weg – er führt über die Teilung einer Strecke in ${\displaystyle n}$ gleich lange Teile und die anschließende Projektion von vier dieser Teile in die gewählte Kurve − zum Auffinden des gesuchten Zentriwinkels.

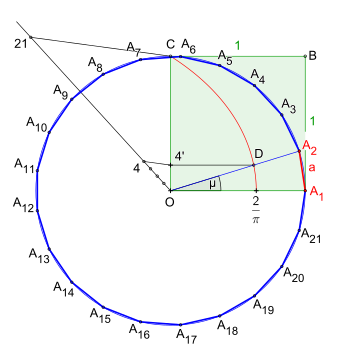
Die Konstruktion des 21‐Ecks bei vorgegebenem Umkreis (Bild 1) nutzt als Konstruktionselement, wie auch im Dreizehneck zu sehen ist, die Quadratrix des Hippias als zusätzliches Hilfsmittel.

Nach dem Zeichnen des Quadrates z. B. mit der Seitenlänge ${\displaystyle 1}$ und der Konstruktion der speziellen Kurve, der sogenannten Quadratrix des Hippias,^[2] mit der Parameterdarstellung ${\displaystyle \gamma \colon (-\pi ,\pi )\to \mathbb {R} ^{2}}$:^[3][4]

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}t\cot \left({\frac {\pi }{2}}t\right)\\t\end{pmatrix}},\quad 0\leq t\leq 1}$

wird die Strecke ${\displaystyle {\overline {CO}}}$ in einundzwanzig gleich lange Abschnitte mithilfe der Streckenteilung geteilt. Aus Gründen der Übersichtlichkeit sind in der Zeichnung nur die relevanten Punkte dargestellt.

Der Zentriwinkel des 21‐Ecks ergibt sich aus ${\displaystyle \mu ={\tfrac {360^{\circ }}{21}},}$ aber die Quadratrix des Hippias unterteilt nur die Winkel ab ${\displaystyle >0^{\circ }}$ bis ${\displaystyle \leq 90^{\circ }}$ in gleich große Winkel. Daraus folgt, ein Einundzwanzigstel der Strecke ${\displaystyle {\overline {CO}}}$ kann nur ein Einundzwanzigstel des Winkels ${\displaystyle 90^{\circ }}$ erzielen. Deshalb wird wegen der Berechnung des Zentriwinkels ${\displaystyle \mu }$ aus dem Umkreis mit seinen ${\displaystyle 360^{\circ }}$ das Vierfache eines Einundzwanzigstels, d. h. der Teilungspunkt ${\displaystyle 4'}$ der Strecke ${\displaystyle {\overline {CO}},}$ zur Konstruktion des Zentriwinkels ${\displaystyle \mu }$ genutzt. Dieser entsteht nach der Konstruktion einer Parallelen zu ${\displaystyle {\overline {A_{1}O}}}$ ab ${\displaystyle 4'}$ bis zur Kurve der Quadratrix, dabei ergibt sich der Punkt ${\displaystyle D}$. Nun zieht man eine Halbgerade ab dem Winkelscheitel ${\displaystyle O}$ durch ${\displaystyle D}$ bis zum Umkreis.

Somit ergibt sich der Zentriwinkel ${\displaystyle \mu }$ und auf dem Umkreis der zweite Eckpunkt ${\displaystyle A_{2}}$. Die Länge der Strecke ${\displaystyle {\overline {A_{1}A_{2}}}}$ ist die exakte Seitenlänge ${\displaystyle a}$ des regelmäßigen 21‐Ecks mit vorgegebenem Umkreis.

Die Konstruktion des 21‐Ecks bei vorgegebener Seitenlänge ${\displaystyle a}$ wie im (Bild 2) dargestellt, ist quasi die Weiterführung der Konstruktion des 21‐Ecks Bei vorgegebenem Umkreis (Bild 1). Sie nutzt ebenfalls als Konstruktionselement die Quadratrix des Hippias als zusätzliches Hilfsmittel. Die vorgegebene Seitenlänge ${\displaystyle a}$ ist, je nach Betrachtungsweise, als zentrische Streckung des Umkreises des 21‐Ecks^[5] mit sogenanntem negativen Streckungsfaktor bzw. als geometrische Ähnlichkeit zweier Dreiecke eingearbeitet.

Bei Berücksichtigung, dass die Punkte ${\displaystyle A}$ und ${\displaystyle E}$ im Bild 2 den Punkten ${\displaystyle A_{1}}$ und ${\displaystyle A_{2}}$ im Bild 1 entsprechen, kann die Konstruktionsbeschreibung des 21‐Ecks Bei vorgegebenem Umkreis vollständig übernommen werden.

Es bedarf nun lediglich einer Winkelhalbierenden ${\displaystyle (wh)}$ des Zentriwinkels ${\displaystyle \mu ,}$ darauf eines Kreises mit dem Durchmesser ${\displaystyle {\overline {GH}}}$ gleich der gegebenen Seitenlänge ${\displaystyle a}$ um Punkt ${\displaystyle F}$ und schließlich zweier Parallelen zu ${\displaystyle wh,}$ je eine ab ${\displaystyle G}$ und ${\displaystyle H,}$ bis zu den Winkelschenkeln des Zentriwinkels.

Die sich somit ergebenden Schnittpunkte ${\displaystyle A_{1}}$ und ${\displaystyle A_{2}}$ sind die ersten beiden Eckpunkte und die Strecke ${\displaystyle {\overline {OA_{1}}}}$ der exakte Umkreisradius des 21‐Ecks mit vorgegebener Seitenlänge.

Ein regelmäßiges überschlagenes 21‐Eck ergibt sich, wenn beim Verbinden der einundzwanzig Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

Es gibt nur fünf regelmäßige Einundzwanzigstrahlsterne.

Die „Sterne“ mit den Symbolen {21/3} und {21/18} sind regelmäßige Siebenecke, {21/6} und {21/15} sowie {21/9} und {21/12} sind regelmäßige Heptagramme, {21/7} und {21/14} sind gleichseitige Dreiecke.

• Regelmäßige Einundzwanzigstrahlsterne
• 
  ${\displaystyle \left\{21/2\right\}{,}\ \left\{21/19\right\}}$
• 
  ${\displaystyle \left\{21/4\right\}{,}\ \left\{21/17\right\}}$
• 
  ${\displaystyle \left\{21/5\right\}{,}\ \left\{21/16\right\}}$
• 
  ${\displaystyle \left\{21/8\right\}{,}\ \left\{21/13\right\}}$
• 
  ${\displaystyle \left\{21/10\right\}{,}\ \left\{21/11\right\}}$

Wiktionary: Einundzwanzigeck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

1. ↑ Henry George Liddell, Robert Scott: A Greek-English Lexicon. Abgerufen am 2. Juli 2024. 
2. ↑ Rieke Deimer: Die Quadratrix. In: Mathematik / Algebraische Geometrie, Ausgewaehlte hoehere Kurven WS2016-17. Universität Mainz, 6. Januar 2017, abgerufen am 8. September 2018. 
3. ↑ Hans-Wolfgang Henn: Elementare Geometrie und Algebra. Verlag Vieweg+Teubner, 2003, S. 45–48. Seite 46 ff. Quadratrix (Auszug (Google)), abgerufen am 8. September 2018.
4. ↑ Horst Hischer: Mathematik in der Schule 32 (1994) 5. Geschichte der Mathematik als didaktischer Aspekt (2). Lösung klassischer Probleme. S. 279 ff., abgerufen am 8. September 2018. 
5. ↑ Friedhelm Kürpig Oliver Niewiadomski: Grundlehre Geometrie Begriffe, Lehrsätze, Grundkonstruktionen; Verlag Friedr. Vieweg & Sohn, 1992 Seite 61 Zentrische Streckung (Auszug (Google)), abgerufen am 8. September 2018.