In der Mathematik ist das logarithmische Mittel, also der logarithmische Mittelwert, ein bestimmter Mittelwert, der die Logarithmusfunktion verwendet.
Definition
Das logarithmische Mittel  zweier verschiedener positivreeller Zahlen
zweier verschiedener positivreeller Zahlen  ist gegeben durch
ist gegeben durch

Um auch den Fall  zu erfassen, definiert man allgemeiner
zu erfassen, definiert man allgemeiner

Dann ist  .
.
Eigenschaften
Das logarithmische Mittel ist eine streng monoton wachsende Funktion. Ferner liegt das logarithmische Mittel zwischen dem arithmetischen und geometrischen Mittel:
 [1]
[1]
Diese Ungleichung gilt für  .
.
Der Beweis stützt sich auf die grafische Veranschaulichung des zugrunde liegenden Sachverhalts (Figur 1 und Figur 2). Wegen der schon vergebenen Bezeichnungen  und
und  für die Koordinatenachsen werden hier die positiven reellen Zahlen
für die Koordinatenachsen werden hier die positiven reellen Zahlen  und
und  mit
mit  vorgegeben.[2][3]
vorgegeben.[2][3]
Aus Figur 1 resultiert der erste Beweisansatz
 .
.
Nach Stammfunktionsbildung folgt hieraus zunächst

und schließlich nach einer elementaren Ungleichungsoperation
 ,
,
womit der rechte Teil der Ungleichung bewiesen ist.
Der zweite Beweisansatz wird aus Figur 2 ersichtlich:

Wieder ergibt sich nach Lösen des Integrals und mehreren Äquivalenzumformungen

und abschließend
 .
.
Damit ist auch der linke Teil der Ungleichung bewiesen.
Anwendungen
Der logarithmische Mittelwert findet in diversen Wissenschaften und technischen Problemen Verwendung. Es tritt meist dann auf, wenn über treibende Gefälle gemittelt wird. Dies ist zum Beispiel bei der integralen Betrachtung von Wärme- oder Stofftransportprozessen der Fall, beispielsweise bei der verfahrenstechnischen Auslegung von Wärmetauschern oder Trennkolonnen.
Analysis
Mittelwertsatz
Nach dem Mittelwertsatz der Differentialrechnung gibt es zu einer differenzierbaren Funktion ![{\displaystyle f\colon [x,y]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3938574dbd5068d312b3b9daa51c3d30858295d1) ein
ein ![{\displaystyle \xi \in [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dda0483353166b04a47473960253f9a86c5f9bd) mit
mit

Für  erhält man daraus
erhält man daraus
 , also
, also  .
.
Das  ist in diesem Fall also der logarithmische Mittelwert aus
ist in diesem Fall also der logarithmische Mittelwert aus  und
und  .
.
Integration
Außerdem erhält man für die Integration

Verallgemeinerungen
Mehrere Variablen
Die Verallgemeinerungen des logarithmischen Mittels auf mehr als zwei Variablen wird seltener verwendet und ist uneinheitlich.
Verallgemeinert man die Idee des Mittelwertsatzes etwa ist
![{\displaystyle L_{\mathrm {MV} }(x_{0},\dots ,x_{n})={\sqrt[{-n}]{(-1)^{(n+1)}\cdot n\cdot \ln[x_{0},\dots ,x_{n}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bf2da92bb33e958e99990d0fbfba8401582688b)
wobei ![{\displaystyle \ln[x_{0},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e27804c54a474fa8510e222a73dfe384294cebcc) die dividierten Differenzen des Logarithmus bezeichnen.
die dividierten Differenzen des Logarithmus bezeichnen.
Für  , also für drei Variablen, führt dies zu
, also für drei Variablen, führt dies zu
 .
.
Verallgemeinert man das Integral zu

mit  erhielte man
erhielte man
![{\displaystyle L_{\mathrm {I} }(x_{0},\dots ,x_{n})=n!\cdot \exp[\ln x_{0},\dots ,\ln x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2444651f6db9ee9128bb9985d009487f82f3a3b)
und als Spezialfall für drei Variablen
 .
.
Andere Mittelwerte
Das Stolarsky-Mittel etwa verallgemeinert das logarithmische Mittel.
Quellen
- Horst Alzer: Ungleichungen für Mittelwerte. Archiv der Mathematik, Vol 47, Nr. 5 / Nov. 1986, doi:10.1007/BF01189983.
- A. O. Pittenger: The logarithmic mean in n variables. In: American Mathematical Monthly, 92 (1985), S. 99–104.
- Gao Jia, Jinde Cao: A New Upper Bound of the Logarithmic Mean. Journal of Inequalities in Pure and Applied Mathematics 4, 4, 2003, 80.
Einzelnachweise
- ↑ Eric W. Weisstein: Arithmetic-Logarithmic-Geometric-Mean-Inequality und Napier's Inequality in MathWorld
- ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 142
- ↑ Mathematics Magazine, vol. 68, no. 4 (Oct. 1995), S. 305
 Figur 1
Figur 1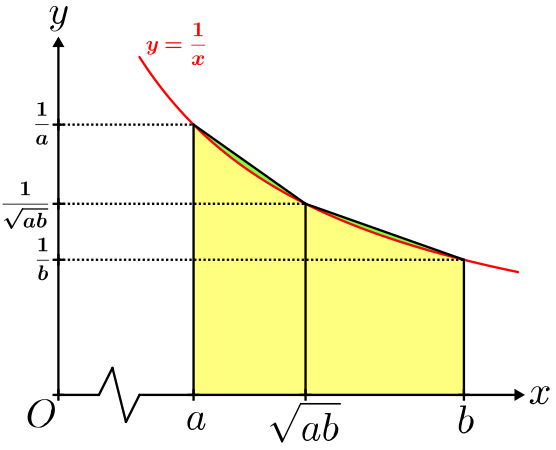 Figur 2
Figur 2




















![{\displaystyle f\colon [x,y]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3938574dbd5068d312b3b9daa51c3d30858295d1)
![{\displaystyle \xi \in [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dda0483353166b04a47473960253f9a86c5f9bd)






![{\displaystyle L_{\mathrm {MV} }(x_{0},\dots ,x_{n})={\sqrt[{-n}]{(-1)^{(n+1)}\cdot n\cdot \ln[x_{0},\dots ,x_{n}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bf2da92bb33e958e99990d0fbfba8401582688b)
![{\displaystyle \ln[x_{0},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e27804c54a474fa8510e222a73dfe384294cebcc)




![{\displaystyle L_{\mathrm {I} }(x_{0},\dots ,x_{n})=n!\cdot \exp[\ln x_{0},\dots ,\ln x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2444651f6db9ee9128bb9985d009487f82f3a3b)











