Stabilitätsfunktion

Die Stabilitätsfunktion ist in der Numerik ein Hilfsmittel, um Lösungsverfahren für gewöhnliche Differentialgleichungen zu analysieren. Die einfache Testgleichung von Germund Dahlquist ${\displaystyle y'(t)=\lambda y(t),\ y(0)=1}$ mit ${\displaystyle \lambda \in \mathbb {C} }$ besitzt als Lösung die Exponentialfunktion ${\displaystyle y(t)=e^{\lambda t}}$. Bei den meisten Verfahren für gewöhnliche Differentialgleichungen kann man die berechnete Näherungslösung nach einem Zeitschritt mit einer Schrittweite ${\displaystyle h}$ ebenfalls als eine Funktion schreiben, die nur vom Produkt ${\displaystyle z=h\lambda \in \mathbb {C} }$ abhängt. Diese Funktion ist die Stabilitätsfunktion und wird oft mit ${\displaystyle R(z)}$ bezeichnet. Durch einen Vergleich mit der Exponentialfunktion ${\displaystyle e^{z}=e^{h\lambda }}$ bekommt man grundlegende Informationen über das numerische Verfahren. So beziehen sich einige Stabilitätsbegriffe auf die Eigenschaften von ${\displaystyle R(z)}$.

Mit Hilfe der Stabilitätsfunktion ${\displaystyle R(z)}$ lässt sich das Stabilitätsgebiet ${\displaystyle S}$ beschreiben und berechnen in der Form

${\displaystyle S=\{z\in \mathbb {C} :|R(z)|<1\}.}$

Denn bei Einschrittverfahren gilt für die Näherungen ${\displaystyle y_{n}}$ zum Zeitpunkt ${\displaystyle t_{n}=nh}$ die Beziehung ${\displaystyle y_{n}=R(z)y_{n-1}=\ldots =\left(R(z)\right)^{j}y_{n-j}=\ldots =\left(R(z)\right)^{n}y_{0}}$ und daher gilt

${\displaystyle y_{n}{\xrightarrow {n\to \infty }}0\iff z\in S.}$

Wenn ${\displaystyle S}$ die ganze linke komplexe Halbebene umfasst, heißt das Verfahren A-stabil. Dann ist der Betrag von ${\displaystyle R}$ in der ganzen offenen linken Halbebene kleiner als 1. Besonders günstig für ein Verfahren ist es, wenn ${\displaystyle R(z)}$ außerdem noch den Grenzwert 0 hat, wenn ${\displaystyle z}$ auf der reellen Achse gegen ${\displaystyle -\infty }$ strebt, sodass sich also der Betrag von ${\displaystyle R(z)}$ dort asymptotisch wie die Exponentialfunktion verhält. Dann heißt das Verfahren L-stabil.

Das explizite Euler-Verfahren ${\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n})}$ ergibt für die Testgleichung mit ${\displaystyle f(t,y)=\lambda y}$ nach einem Schritt

${\displaystyle y_{1}=y_{0}+h\lambda y_{0}=(1+h\lambda )y_{0}}$,

also gilt für seine Stabilitätsfunktion ${\displaystyle R(z)=1+z}$. Sein Stabilitätsgebiet besteht daher aus allen komplexen Zahlen ${\displaystyle z}$ mit ${\displaystyle |1+z|<1}$, was dem Inneren des Kreises mit Mittelpunkt ${\displaystyle -1}$ und Radius ${\displaystyle 1}$ in der komplexen Zahlenebene entspricht.

Für das implizite Euler-Verfahren ${\displaystyle y_{n+1}=y_{n}+hf(t_{n+1},y_{n+1})}$ folgt dagegen mit ${\displaystyle f(t,y)=\lambda y}$

${\displaystyle y_{1}=y_{0}+h\lambda y_{1}\iff y_{1}={\frac {1}{1-h\lambda }}y_{0}}$,

also ${\displaystyle R(z)={\frac {1}{1-z}}}$. Das Stabilitätsgebiet ist nun durch die Bedingung ${\displaystyle |{\tfrac {1}{1-z}}|<1}$ gegeben, die mit

${\displaystyle |1-z|>1}$

gleichwertig ist, was dem Äußeren des Kreises mit Mittelpunkt ${\displaystyle 1}$ und Radius ${\displaystyle 1}$ entspricht. Es enthält daher die ganze offene linke Halbebene und somit ist das implizite Euler-Verfahren A-stabil. Wegen ${\displaystyle \lim _{z\to -\infty }{\frac {1}{1-z}}=0}$ ist es sogar L-stabil.

Runge-Kutta-Verfahren sind vollständig durch die Koeffizienten ${\displaystyle A,b,c}$ aus ihrem Butcher-Tableau festgelegt. Bei der Testgleichung ist der Anfangswert ${\displaystyle y_{0}=1}$ und für die Stufen ergibt sich im ersten Zeitschritt

${\displaystyle k_{i}=\lambda \left(1+h\sum _{j=1}^{s}a_{ij}k_{j}\right),\quad i=1,\dotsc ,s.}$

Dies ist ein quadratisches lineares Gleichungssystem für den Vektor ${\displaystyle k=(k_{1},\dotsc ,k_{s})^{T}}$ in der Form ${\displaystyle (I-zA)k=\lambda e}$ mit dem Vektor ${\displaystyle e=(1,\dotsc ,1)^{T}.}$ Mit dessen Lösung bekommt man dann die Runge-Kutta-Näherung ${\displaystyle y_{1}\approx y(h)}$ in der Form

${\displaystyle y_{1}=y_{0}+h\sum _{j=1}^{s}b_{j}k_{j}=1+hb^{T}k=1+zb^{T}(I-zA)^{-1}e=:R(z).}$

Dies ist bei Runge-Kutta-Verfahren eine rationale Funktion, daher wird sie gerne mit ${\displaystyle R(z)}$ bezeichnet.

Bei expliziten Runge-Kutta-Verfahren ist die Koeffizientenmatrix ${\displaystyle A}$ eine strikt untere Dreiecksmatrix, daher bricht die Neumann-Reihe von ${\displaystyle (I-zA)^{-1}}$ nach s${\displaystyle }$ Summanden ab und man bekommt

${\displaystyle R(z)=1+zb^{T}(I-zA)^{-1}e=1+zb^{T}e+z^{2}b^{T}Ae+\dotsb +z^{s}b^{T}A^{s-1}e.}$

Daher ist die Stabilitätsfunktion eines expliziten Runge-Kutta-Verfahrens ein Polynom, solche Verfahren können nicht A-stabil sein.

Bei impliziten Runge-Kutta-Verfahren sind aber z. B. die Gauß-Legendre-Verfahren A-stabil. Die Stabilitätsfunktionen dieser speziellen Verfahren sind sogar sehr gute Approximationen an die Exponentialfunktion, nämlich die sogenannten Padé-Approximationen.

Wendet man ein lineares Mehrschrittverfahren ${\displaystyle \sum _{j=0}^{m}\alpha _{j}y_{n-j}=h\sum _{j=0}^{m}\beta _{j}f(y_{n-j})}$ auf die Testgleichung an, ergibt sich wieder mit ${\displaystyle z=h\lambda }$ die Gleichung

${\displaystyle \sum _{j=0}^{m}\alpha _{j}y_{n-j}-z\sum _{j=0}^{m}\beta _{j}y_{n-j}=\sum _{j=0}^{m}(\alpha _{j}-z\beta _{j})y_{n-j}=0.}$

Dies ist eine lineare Differenzengleichung, die man einfach lösen kann. Denn die Folge ${\displaystyle y_{n}=u^{n}}$ ist eine nichttriviale Lösung dieser Differenzengleichung, wenn u eine Nullstelle des charakteristischen Polynoms

${\displaystyle 0{\stackrel {!}{=}}\sum _{j=0}^{m}\alpha _{j}u^{m-j}-z\sum _{j=0}^{m}\beta _{j}u^{m-j}=\varrho (u)-z\sigma (u)}$

ist, wobei man die Polynome

${\displaystyle \varrho (u)=\sum _{j=0}^{m}\alpha _{j}u^{m-j}}$

${\displaystyle \sigma (u)=\sum _{j=0}^{m}\beta _{j}u^{m-j}}$

eingeführt hat. Also bekommt man mit den von ${\displaystyle z}$ abhängenden Nullstellen ${\displaystyle u}$ des Polynoms ${\displaystyle \varrho (u)-z\sigma (u)}$ die Lösungen ${\displaystyle u^{n}}$ zur Testgleichung und daher liegt ${\displaystyle z}$ im Stabilitätsgebiet des Verfahrens, wenn alle diese Lösungen gegen 0 gehen für ${\displaystyle n\to \infty }$. Daher kann man die betragsmaximale Nullstelle ${\displaystyle |u(z)|}$ als Stabilitätsfunktion des Verfahrens ansehen.

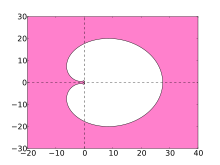
Diese Interpretation erscheint sehr unhandlich. Allerdings interessiert man sich oft weniger für die Stabilitätsfunktion, sondern für das Stabilitätsgebiet ${\displaystyle S}$. Der Rand dieses Gebietes besteht aus denjenigen ${\displaystyle z\in \mathbb {C} }$, bei dem für die Nullstellen ${\displaystyle |u|=1}$ gilt, wo die Nullstellen also auf dem komplexen Einheitskreis liegen. Da ${\displaystyle \varrho (u)-z\sigma (u)=0\Leftarrow z=\varrho (u)/\sigma (u)}$ gilt, ist die Bestimmung des Stabilitätsgebiets bei Mehrschrittverfahren sogar besonders einfach, denn seinen Rand erhält man i. W. explizit durch

${\displaystyle \partial S={\Big \{}{\frac {\varrho (u)}{\sigma (u)}}:\,|u|=1{\Big \}}={\Big \{}{\frac {\varrho (e^{i\varphi })}{\sigma (e^{i\varphi })}}:\,\varphi \in [0,2\pi ){\Big \}}.}$

Als Beispiel wird das Stabilitätsgebiet für das 6-stufige BDF-Verfahren gezeigt.

Obwohl auch Mehrschrittverfahren in der Gestalt von allgemeinen linearen Verfahren geschrieben werden können, ist die Struktur ähnlich derjenigen der Runge-Kutta-Verfahren weiter oben. Daher bekommt man ein ähnliches Ergebnis. Für den Vektor ${\displaystyle Y}$ der Stufenlösungen gilt

${\displaystyle Y=zAY+Uy^{[n-1]}\quad \Rightarrow Y=(I-zA)^{-1}Uy^{[n-1]}}$

und der Zeitschritt wird daher zu

${\displaystyle y^{[n]}=zBY+Vy^{[n-1]}=(V+zB(I-zA)^{-1}U{\big )}y^{[n-1]}.}$

In jedem Zeitschritt erfolgt also die Multiplikation mit derselben Matrix

${\displaystyle M(z)=V+zB(I-zA)^{-1}U.}$

Es gilt daher ${\displaystyle y^{[n]}=M(z)^{n}y^{[0]}\to 0\,(n\to \infty )}$, wenn die Potenzen von ${\displaystyle M(z)}$ gegen 0 gehen, also alle Eigenwerte von ${\displaystyle M(z)}$ innerhalb des komplexen Einheitskreises liegen. Daher kann man hier den Spektralradius von ${\displaystyle M(z)}$ als Stabilitätsfunktion ${\displaystyle R(z)}$ in der Definition des Stabilitätsgebiets ${\displaystyle S}$ ansehen.

Die obige Testgleichung von Dahlquist ist sehr einfach, hat aber eine weitergehende Bedeutung für Systeme von linearen, autonomen und homogenen Differentialgleichungen

${\displaystyle y'(t)=Qy(t),\quad y(0)=y_{0},\quad Q\in \mathbb {R} ^{d\times d}.}$

Die exakte Lösung ist ${\displaystyle y(t)=e^{tQ}y_{0}}$ mit dem Matrixexponential ${\displaystyle e^{tQ}}$. Die numerische Lösung ${\displaystyle y_{n}}$ kann man jetzt mit der Matrix-Stabilitätsfunktion ${\displaystyle R(tQ)}$ darstellen. Wenn dabei ${\displaystyle J=P^{-1}QP}$ die Jordan-Normalform von ${\displaystyle Q\ (=PJP^{-1})}$ ist, gilt

${\displaystyle y_{n}={\big (}R(hQ){\big )}^{n}y_{0}=P{\big (}R(hJ){\big )}^{n}P^{-1}y_{0}.}$

Bei einer diagonalisierbaren Matrix ${\displaystyle Q}$ ist, ist ${\displaystyle R(hJ)}$ eine Diagonalmatrix mit den Diagonalelementen ${\displaystyle R(h\lambda _{j})}$. Wenn für alle Eigenwerte ${\displaystyle \lambda _{j}}$ von ${\displaystyle Q}$ gilt, dass ${\displaystyle h\lambda _{j}\in S}$ ist, dann konvergiert auch hier ${\displaystyle y_{n}\to 0\,(n\to \infty )}$. Bei dieser Differentialgleichung sieht man gleichzeitig, dass es sinnvoll ist, ${\displaystyle S}$ als offene Menge zu definieren. Denn im diagonalisierbaren Fall bleiben zwar Lösungen auf dem Rand mit ${\displaystyle h\lambda _{j}\in \partial S}$ noch beschränkt, aber im Allgemeinen nicht mehr, wenn mehrfache Eigenwerte mit Jordanblöcken auftreten.

• E. Hairer, G. Wanner: Solving Ordinary Differential Equations II, Stiff problems. Springer Verlag.
• K. Strehmel, R. Weiner, H. Podhaisky: Numerik gewöhnlicher Differentialgleichungen – Nichtsteife, steife und differential-algebraische Gleichungen. Springer Spektrum, 2012.