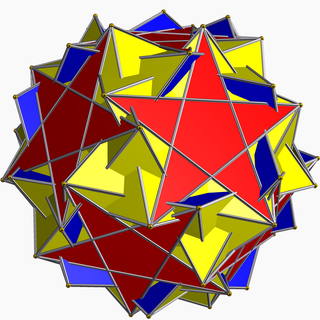
Inverted snub dodecadodecahedron

Inverted snub dodecadodecahedron
Type	Uniform star polyhedron
Elements	F = 84, E = 150 V = 60 (χ = −6)
Faces by sides	60{3}+12{5}+12{5/2}
Coxeter diagram
Wythoff symbol	| 5/3 2 5
Symmetry group	I, [5,3]+, 532
Index references	U60, C76, W114
Dual polyhedron	Medial inverted pentagonal hexecontahedron
Vertex figure	3.3.5.3.5/3
Bowers acronym	Isdid

In geometry, the inverted snub dodecadodecahedron (or vertisnub dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U₆₀.^[1] It is given a Schläfli symbol sr{5/3,5}.

Let ${\displaystyle \xi \approx 2.109759446579943}$ be the largest real zero of the polynomial ${\displaystyle P=2x^{4}-5x^{3}+3x+1}$. Denote by ${\displaystyle \phi }$ the golden ratio. Let the point ${\displaystyle p}$ be given by

${\displaystyle p={\begin{pmatrix}\phi ^{-2}\xi ^{2}-\phi ^{-2}\xi +\phi ^{-1}\\-\phi ^{2}\xi ^{2}+\phi ^{2}\xi +\phi \\\xi ^{2}+\xi \end{pmatrix}}}$.

Let the matrix ${\displaystyle M}$ be given by

${\displaystyle M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}}$.

${\displaystyle M}$ is the rotation around the axis ${\displaystyle (1,0,\phi )}$ by an angle of ${\displaystyle 2\pi /5}$, counterclockwise. Let the linear transformations ${\displaystyle T_{0},\ldots ,T_{11}}$ be the transformations which send a point ${\displaystyle (x,y,z)}$ to the even permutations of ${\displaystyle (\pm x,\pm y,\pm z)}$ with an even number of minus signs. The transformations ${\displaystyle T_{i}}$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations ${\displaystyle T_{i}M^{j}}$ ${\displaystyle (i=0,\ldots ,11}$, ${\displaystyle j=0,\ldots ,4)}$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points ${\displaystyle T_{i}M^{j}p}$ are the vertices of a snub dodecadodecahedron. The edge length equals ${\displaystyle 2(\xi +1){\sqrt {\xi ^{2}-\xi }}}$, the circumradius equals ${\displaystyle (\xi +1){\sqrt {2\xi ^{2}-\xi }}}$, and the midradius equals ${\displaystyle \xi ^{2}+\xi }$.

For a great snub icosidodecahedron whose edge length is 1, the circumradius is

${\displaystyle R={\frac {1}{2}}{\sqrt {\frac {2\xi -1}{\xi -1}}}\approx 0.8516302281174128}$

Its midradius is

${\displaystyle r={\frac {1}{2}}{\sqrt {\frac {\xi }{\xi -1}}}\approx 0.6894012223976083}$

The other real root of P plays a similar role in the description of the Snub dodecadodecahedron

Medial inverted pentagonal hexecontahedron
Type	Star polyhedron
Face
Elements	F = 60, E = 150 V = 84 (χ = −6)
Symmetry group	I, [5,3]+, 532
Index references	DU60
dual polyhedron	Inverted snub dodecadodecahedron

The medial inverted pentagonal hexecontahedron (or midly petaloid ditriacontahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform inverted snub dodecadodecahedron. Its faces are irregular nonconvex pentagons, with one very acute angle.

Denote the golden ratio by ${\displaystyle \phi }$, and let ${\displaystyle \xi \approx -0.236\,993\,843\,45}$ be the largest (least negative) real zero of the polynomial ${\displaystyle P=8x^{4}-12x^{3}+5x+1}$. Then each face has three equal angles of ${\displaystyle \arccos(\xi )\approx 103.709\,182\,219\,53^{\circ }}$, one of ${\displaystyle \arccos(\phi ^{2}\xi +\phi )\approx 3.990\,130\,423\,41^{\circ }}$ and one of ${\displaystyle 360^{\circ }-\arccos(\phi ^{-2}\xi -\phi ^{-1})\approx 224.882\,322\,917\,99^{\circ }}$. Each face has one medium length edge, two short and two long ones. If the medium length is ${\displaystyle 2}$, then the short edges have length $${\displaystyle 1-{\sqrt {\frac {1-\xi }{\phi ^{3}-\xi }}}\approx 0.474\,126\,460\,54,}$$ and the long edges have length $${\displaystyle 1+{\sqrt {\frac {1-\xi }{\phi ^{-3}-\xi }}}\approx 37.551\,879\,448\,54.}$$ The dihedral angle equals ${\displaystyle \arccos(\xi /(\xi +1))\approx 108.095\,719\,352\,34^{\circ }}$. The other real zero of the polynomial ${\displaystyle P}$ plays a similar role for the medial pentagonal hexecontahedron.

• List of uniform polyhedra
• Snub dodecadodecahedron

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208 p. 124

• Weisstein, Eric W. "Medial inverted pentagonal hexecontahedron". MathWorld.
• Weisstein, Eric W. "Inverted snub dodecadodecahedron". MathWorld.