Lonely runner conjecture

In number theory, specifically the study of Diophantine approximation, the lonely runner conjecture is a conjecture about the long-term behavior of runners on a circular track. It states that ${\displaystyle n}$ runners on a track of unit length, with constant speeds all distinct from one another, will each be lonely at some time—at least ${\displaystyle 1/n}$ units away from all others.

The conjecture was first posed in 1967 by German mathematician Jörg M. Wills, in purely number-theoretic terms, and independently in 1974 by T. W. Cusick; its illustrative and now-popular formulation dates to 1998. The conjecture is known to be true for seven runners or fewer, but the general case remains unsolved. Implications of the conjecture include solutions to view-obstruction problems and bounds on properties, related to chromatic numbers, of certain graphs.

Consider ${\displaystyle n}$ runners on a circular track of unit length. At the initial time ${\displaystyle t=0}$, all runners are at the same position and start to run; the runners' speeds are constant, all distinct, and may be negative. A runner is said to be lonely at time ${\displaystyle t}$ if they are at a distance (measured along the circle) of at least ${\displaystyle 1/n}$ from every other runner. The lonely runner conjecture states that each runner is lonely at some time, no matter the choice of speeds.^[1]

This visual formulation of the conjecture was first published in 1998.^[2] In many formulations, including the original by Jörg M. Wills,^[3][4] some simplifications are made. The runner to be lonely is stationary at 0 (with zero speed), and therefore ${\displaystyle n-1}$ other runners, with nonzero speeds, are considered.^[a] The moving runners may be further restricted to positive speeds only: by symmetry, runners with speeds ${\displaystyle x}$ and ${\displaystyle -x}$ have the same distance from 0 at all times, and so are essentially equivalent. Proving the result for any stationary runner implies the general result for all runners, since they can be made stationary by subtracting their speed from all runners, leaving them with zero speed. The conjecture then states that, for any collection ${\displaystyle v_{1},v_{2},...,v_{n-1}}$ of positive, distinct speeds, there exists some time ${\displaystyle t>0}$ such that $${\displaystyle {\frac {1}{n}}\leq \operatorname {frac} (v_{i}t)\leq 1-{\frac {1}{n}}\qquad (i=1,...,n-1),}$$ where ${\displaystyle \operatorname {frac} (x)}$ denotes the fractional part of ${\displaystyle x}$.^[6] Interpreted visually, if the runners are running counterclockwise, the middle term of the inequality is the distance from the origin to the ${\displaystyle i}$th runner at time ${\displaystyle t}$, measured counterclockwise.^[b] This convention is used for the rest of this article. Wills' conjecture was part of his work in Diophantine approximation,^[7] the study of how closely fractions can approximate irrational numbers.

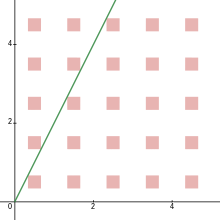
Suppose ${\displaystyle C}$ is a n-hypercube of side length ${\displaystyle s}$ in n-dimensional space (${\displaystyle n\geq 2}$). Place a centered copy of ${\displaystyle C}$ at every point with half-integer coordinates. A ray from the origin may either miss all of the copies of ${\displaystyle C}$, in which case there is a (infinitesimal) gap, or hit at least one copy. Cusick (1973) made an independent formulation of the lonely runner conjecture in this context; the conjecture implies that there are gaps if and only if ${\displaystyle s<(n-1)/(n+1)}$, ignoring rays lying in one of the coordinate hyperplanes.^[8] For example, placed in 2-dimensional space, squares any smaller than ${\displaystyle 1/3}$ in side length will leave gaps, as shown, and squares with side length ${\displaystyle 1/3}$ or greater will obstruct every ray that is not parallel to an axis. The conjecture generalizes this observation into any number of dimensions.

In graph theory, a distance graph ${\displaystyle G}$ on the set of integers, and using some finite set ${\displaystyle D}$ of positive integer distances, has an edge between ${\displaystyle x,y}$ if and only if ${\displaystyle |x-y|\in D}$. For example, if ${\displaystyle D=\{2\}}$, every consecutive pair of even integers, and of odd integers, is adjacent, all together forming two connected components. A k-regular coloring of the integers with step ${\displaystyle \lambda \in \mathbb {R} }$ assigns to each integer ${\displaystyle n}$ one of ${\displaystyle k}$ colors based on the residue of ${\displaystyle \lfloor \lambda n\rfloor }$modulo ${\displaystyle k}$. For example, if ${\displaystyle \lambda =0.5}$, the coloring repeats every ${\displaystyle 2k}$ integers and each pair of integers ${\displaystyle 2m,2m+1}$ are the same color. Taking ${\displaystyle k=|D|+1}$, the lonely runner conjecture implies ${\displaystyle G}$ admits a proper k-regular coloring (i.e., each node is colored differently than its adjacencies) for some step value.^[9] For example, ${\displaystyle (k,\lambda )=(2,0.5)}$ generates a proper coloring on the distance graph generated by ${\displaystyle D=\{2\}}$. (${\displaystyle k}$ is known as the regular chromatic number of ${\displaystyle D}$.)

Given a directed graph ${\displaystyle G}$, a nowhere-zero flow on ${\displaystyle G}$ associates a positive value ${\displaystyle f(e)}$ to each edge ${\displaystyle e}$, such that the flow outward from each node is equal to the flow inward. The lonely runner conjecture implies that, if ${\displaystyle G}$ has a nowhere-zero flow with at most ${\displaystyle k}$ distinct integer values, then ${\displaystyle G}$ has a nowhere-zero flow with values only in ${\displaystyle \{1,2,\ldots ,k\}}$ (possibly after reversing the directions of some arcs of ${\displaystyle G}$). This result was proven for ${\displaystyle k\geq 5}$ with separate methods, and because the smaller cases of the lonely runner conjecture are settled, the full theorem is proven.^[10]

For a given setup of runners, let ${\displaystyle \delta }$ denote the smallest of the runners' maximum distances of loneliness, and the gap of loneliness^[11] ${\displaystyle \delta _{n}}$ denote the minimum ${\displaystyle \delta }$ across all setups with ${\displaystyle n}$ runners. In this notation, the conjecture asserts that ${\displaystyle \delta _{n}\geq 1/n}$, a bound which, if correct, cannot be improved. For example, if the runner to be lonely is stationary and speeds ${\displaystyle v_{i}=i}$ are chosen, then there is no time at which they are strictly more than ${\displaystyle 1/n}$ units away from all others, showing that ${\displaystyle \delta _{n}\leq 1/n}$.^[c] Alternatively, this conclusion can be quickly derived from the Dirichlet approximation theorem. For ${\displaystyle n\geq 2}$ a simple lower bound ${\displaystyle \delta _{n}\geq 1/(2n-2)}$ may be obtained via a probability argument.^[12]

The conjecture can be reduced to restricting the runners' speeds to positive integers: If the conjecture is true for ${\displaystyle n}$ runners with integer speeds, it is true for ${\displaystyle n}$ runners with real speeds.^[13]

Slight improvements on the lower bound ${\displaystyle 1/(2n-2)}$ are known. Chen & Cusick (1999) showed for ${\displaystyle n\geq 5}$ that if ${\displaystyle 2n-5}$ is prime, then ${\displaystyle \delta _{n}\geq {\tfrac {1}{2n-5}}}$, and if ${\displaystyle 4n-9}$ is prime, then ${\displaystyle \delta _{n}\geq {\tfrac {2}{4n-9}}}$. Perarnau & Serra (2016) showed unconditionally for sufficiently large ${\displaystyle n}$ that $${\displaystyle \delta _{n}\geq {\frac {1}{2n-4+o(1)}}.}$$

Tao (2018) proved the current best known asymptotic result: for sufficiently large ${\displaystyle n}$, $${\displaystyle \delta _{n}\geq {\frac {1}{2n-2}}+{\frac {c\log n}{n^{2}(\log \log n)^{2}}}}$$ for some constant ${\displaystyle c>0}$. He also showed that the full conjecture is implied by proving the conjecture for integer speeds of size ${\displaystyle n^{O(n^{2})}}$ (see big O notation). This implication theoretically allows proving the conjecture for a given ${\displaystyle n}$ by checking a finite set of cases, but the number of cases grows too quickly to be practical.^[14]

The conjecture has been proven under specific assumptions on the runners' speeds. For sufficiently large ${\displaystyle n}$, it holds true if $${\displaystyle {\frac {v_{i+1}}{v_{i}}}\geq 1+{\frac {22\log(n-1)}{n-1}}\qquad (i=1,...,n-2).}$$ In other words, the conjecture holds true for large ${\displaystyle n}$ if the speeds grow quickly enough. If the constant 22 is replaced with 33, then the conjecture holds true for ${\displaystyle n\geq 16343}$.^[15] A similar result for sufficiently large ${\displaystyle n}$ only requires a similar assumption for ${\displaystyle i=\lfloor n/22\rfloor -1,...,n-2}$.^[14] Unconditionally on ${\displaystyle n}$, the conjecture is true if ${\displaystyle v_{i+1}/v_{i}\geq 2}$ for all ${\displaystyle i}$.^[16]

The conjecture is true for ${\displaystyle n\leq 7}$ runners. The proofs for ${\displaystyle n\leq 3}$ are elementary; the ${\displaystyle n=4}$ case was established in 1972.^[17] The ${\displaystyle n=5}$, ${\displaystyle n=6}$, and ${\displaystyle n=7}$ cases were settled in 1984, 2001 and 2008, respectively. The first proof for ${\displaystyle n=5}$ was computer-assisted, but all cases have since been proved with elementary methods.^[18]

For some ${\displaystyle n}$, there exist sporadic examples with a maximum separation of ${\displaystyle 1/n}$ besides the example of ${\displaystyle v_{i}=i}$ given above.^[6] For ${\displaystyle n=5}$, the only known example (up to shifts and scaling) is ${\displaystyle \{0,1,3,4,7\}}$; for ${\displaystyle n=6}$ the only known example is ${\displaystyle \{0,1,3,4,5,9\}}$; and for ${\displaystyle n=8}$ the known examples are ${\displaystyle \{0,1,4,5,6,7,11,13\}}$ and ${\displaystyle \{0,1,2,3,4,5,7,12\}}$.^[19] There exists an explicit infinite family of such sporadic cases.^[20]

Kravitz (2021) formulated a sharper version of the conjecture that addresses near-equality cases. More specifically, he conjectures that for a given set of speeds ${\displaystyle v_{i}}$, either ${\displaystyle \delta =s/(s(n-1)+1)}$ for some positive integer ${\displaystyle s}$,^[d] or ${\displaystyle \delta \geq 1/(n-1)}$, where ${\displaystyle \delta }$ is that setup's gap of loneliness. He confirmed this conjecture for ${\displaystyle n\leq 4}$ and a few special cases.

Rifford (2022) addressed the question of the size of the time required for a runner to get lonely. He formulated a stronger conjecture stating that for every integer ${\displaystyle n\geq 3}$ there is a positive integer ${\displaystyle N}$ such that for any collection ${\displaystyle v_{1},v_{2},...,v_{n-1}}$ of positive, distinct speeds, there exists some time ${\displaystyle t>0}$ such that ${\displaystyle \operatorname {frac} (v_{i}t)\in [1/n,1-1/n]}$ for ${\displaystyle i=1,...n-1}$ with $${\displaystyle t\leq {\frac {N}{\operatorname {min} (v_{1},...,v_{n-1})}}.}$$ Rifford confirmed this conjecture for ${\displaystyle n=3,4,5,6}$ and showed that the minimal ${\displaystyle N}$ in each case is given by ${\displaystyle N=1}$ for ${\displaystyle n=3,4,5}$ and ${\displaystyle N=2}$ for ${\displaystyle n=6}$. The latter result (${\displaystyle N=2}$ for ${\displaystyle n=6}$) shows that if we consider six runners starting from ${\displaystyle 0}$ at time ${\displaystyle t=0}$ with constant speeds ${\displaystyle v_{0},v_{1},...,v_{5}}$ with ${\displaystyle v_{0}=0}$ and ${\displaystyle v_{1},...,v_{5}}$ distinct and positive then the static runner is separated by a distance at least ${\displaystyle 1/6}$ from the others during the first two rounds of the slowest non-static runner (but not necessary during the first round).

A much stronger result exists for randomly chosen speeds: using the stationary-runner convention, if ${\displaystyle n}$ and ${\displaystyle \varepsilon >0}$ are fixed and ${\displaystyle n-1}$ runners with nonzero speeds are chosen uniformly at random from ${\displaystyle \{1,2,\ldots ,k\}}$, then ${\displaystyle P(\delta \geq 1/2-\varepsilon )\to 1}$ as ${\displaystyle k\to \infty }$. In other words, runners with random speeds are likely at some point to be "very lonely"—nearly ${\displaystyle 1/2}$ units from the nearest other runner.^[21] The full conjecture is true if "loneliness" is replaced with "almost aloneness", meaning at most one other runner is within ${\displaystyle 1/n}$ of a given runner.^[22] The conjecture has been generalized to an analog in algebraic function fields.^[23]

• Article in the Open Problem Garden no. 4, 551–562.