Escuchar la forma de un tambor

Escuchar la forma de un tambor es inferir información sobre la forma del parche de un tambor a partir del sonido que produce, es decir, de la lista de sobretonos, mediante el uso de la teoría matemática.

"¿Se puede oír la forma de un tambor?" es el título de un artículo de 1966 de Mark Kac en el American Mathematical Monthly, que hizo famosa la pregunta, aunque esta frase en particular se debe al matemático Lipman Bers. Preguntas similares se remontan al físico Arthur Schuster en 1882.^[1]​ Por su artículo, Kac recibió el Premio Lester R. Ford en 1967 y el Premio Chauvenet en 1968.^[2]​

Las frecuencias a las que puede vibrar un parche dependen de su forma. La ecuación de Helmholtz calcula las frecuencias si se conoce la forma. Estas frecuencias son los valores propios del correspondiente operador laplaciano en el espacio. Una cuestión central es si se puede predecir la forma si se conocen las frecuencias; como por ejemplo, si se puede reconocer un triángulo de Reuleaux (con lados curvos) de esta manera.^[3]​ Kac admitió que no sabía si era posible que dos formas diferentes produjeran el mismo conjunto de frecuencias. La pregunta de si las frecuencias determinan la forma fue finalmente respondida negativamente a principios de los años 1990 por Gordon, Webb y Wolpert.

Más formalmente, el tambor se concibe como una membrana elástica cuyos límites están fijados. Se representa como un dominio D en el plano. Denótense por λ_n los autovalores de Dirichlet para D, es decir, los autovalores del problema de Dirichlet para el laplaciano:

${\displaystyle {\begin{cases}\Delta u+\lambda u=0\\u|_{\partial D}=0\end{cases}}}$

Se dice que dos dominios son isoespectrales (u homofónicos) si tienen los mismos valores propios. El término "homofónico" se justifica porque los valores propios de Dirichlet son precisamente los tonos fundamentales que el tambor es capaz de producir, y que aparecen naturalmente como coeficientes de Fourier en la solución de la ecuación de onda con límite fijado.

Por lo tanto, la pregunta puede reformularse como: ¿qué se puede inferir sobre "D" si solo se conocen los valores de λ_n? O, más específicamente: ¿hay dos dominios distintos que sean isoespectrales?

Se pueden formular problemas relacionados para el problema de Dirichlet para el laplaciano en dominios en dimensiones superiores o en variedades de Riemann, así como para otras operadors diferenciales elípticos como el operador de Cauchy-Riemann o el operador de Dirac. Se pueden imponer otras condiciones de contorno además de la condición de Dirichlet, como la condición de frontera de Neumann (véanse como artículos relacionados geometría espectral e isoespectral).

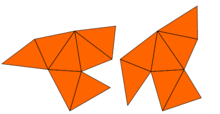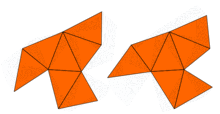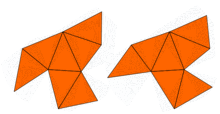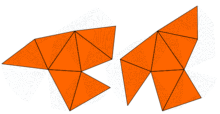
En 1964, John Milnor observó que un teorema sobre redes debido a Ernst Witt implicaba la existencia de un par de toros planos de 16 dimensiones que tienen los mismos valores propios pero formas diferentes. Sin embargo, el problema en dos dimensiones permaneció abierto hasta 1992, cuando Carolyn Gordon, David Webb y Scott Wolpert construyeron, basándose en el método de Sunada, un par de regiones en el plano que tienen formas diferentes pero valores propios idénticos. Las regiones son polígonos cóncavos. La prueba de que ambas regiones tienen los mismos valores propios utiliza las simetrías del laplaciano. Esta idea ha sido generalizada por Buser, Conway, Doyle y Semmler,^[4]​ quienes construyeron numerosos ejemplos similares. Entonces, la respuesta a la pregunta de Kac es: para muchas formas, no se puede escuchar la forma del tambor "completamente". Sin embargo, se puede inferir alguna información.

Por otro lado, Steve Zelditch demostró que la respuesta a la pregunta de Kac es positiva si se imponen restricciones a ciertas regiones planas de Convexidad con límites analíticos. No se sabe si dos dominios analíticos no convexos pueden tener los mismos valores propios. Se sabe que el conjunto de dominios isoespectrales con respecto a uno dado es compacto en la topología C^∞. Además, la esfera (por ejemplo) es espectralmente rígida, por el teorema de comparación de valores propios de Cheng. También se sabe, por un resultado obtenido por Osgood, Phillips y Sarnak, que el espacio de módulos de superficies de Riemann de un género determinado no admite un flujo isoespectral continuo a través de ningún punto y es compacto en la topología de Fréchet-Schwartz.

La fórmula de Weyl establece que se puede inferir el área A del tambor midiendo la rapidez con la que crece λ_n. Se define N(R) como el número de valores propios menores que R, y se obtiene

${\displaystyle A=\omega _{d}^{-1}(2\pi )^{d}\lim _{R\to \infty }{\frac {N(R)}{R^{d/2}}},}$

donde d es la dimensión y ${\displaystyle \omega _{d}}$ es el volumen de la bola unitaria de d dimensiones. Weyl también conjeturó que el siguiente término en la siguiente aproximación daría el perímetro de D. En otras palabras, si L denota la longitud del perímetro (o el área de la superficie en una dimensión superior), entonces se debería tener que

${\displaystyle N(R)=(2\pi )^{-d}\omega _{d}AR^{d/2}\mp {\frac {1}{4}}(2\pi )^{-d+1}\omega _{d-1}LR^{(d-1)/2}+o(R^{(d-1)/2}).}$

Para un límite suave, esto fue demostrado por Victor Ivrii en 1980. Tampoco se permite que la variedad tenga una familia de geodésicas periódicas de dos parámetros, como la que tendría una esfera.

Para límites no suaves, Michael Berry conjeturó en 1979 que la corrección debería ser del orden de ${\displaystyle R^{D/2}}$, donde D es la dimensión de Hausdorff-Besicovitch del límite. Esto fue refutado por J. Brossard y R. A. Carmona, quien luego sugirió que se debería reemplazar la dimensión de Hausdorff por la dimensión de Minkowski-Bouligand. En el plano, esto se demostró cuando el límite tiene dimensión 1 (1993), pero en su mayoría se refutó para dimensiones superiores (1996). Ambos resultados son de Lapidus y Pomerance.

• Triple de Gassmann
• Isoespectral
• Geometría espectral
• Vibraciones de una membrana circular
• Sistema iterativo de funciones, una extensión de los fractales^[5]​

• Abikoff, William (January 1995), «Remembering Lipman Bers», Notices of the American Mathematical Society 42 (1): 8-18 .
• Brossard, Jean; Carmona, René (1986). «Can one hear the dimension of a fractal?». Comm. Math. Phys. 104 (1): 103-122. Bibcode:1986CMaPh.104..103B. S2CID 121173871. doi:10.1007/BF01210795. 
• Buser, Peter; Conway, John; Doyle, Peter; Semmler, Klaus-Dieter (1994), «Some planar isospectral domains», International Mathematics Research Notices 1994 (9): 391-400, doi:10.1155/S1073792894000437 .
• Chapman, S.J. (1995). «Drums that sound the same». American Mathematical Monthly 102 (February): 124-138. JSTOR 2975346. doi:10.2307/2975346. 
• Giraud, Olivier; Thas, Koen (2010). «Hearing shapes of drums – mathematical and physical aspects of isospectrality». Reviews of Modern Physics 82 (3): 2213-2255. Bibcode:2010RvMP...82.2213G. S2CID 119289493. arXiv:1101.1239. doi:10.1103/RevModPhys.82.2213. 
• Gordon, Carolyn; Webb, David (1996), «You can't hear the shape of a drum», American Scientist 84 (January–February): 46-55, Bibcode:1996AmSci..84...46G .
• Gordon, C.; Webb, D.; Wolpert, S. (1992), «Isospectral plane domains and surfaces via Riemannian orbifolds», Inventiones Mathematicae 110 (1): 1-22, Bibcode:1992InMat.110....1G, S2CID 122258115, doi:10.1007/BF01231320 .
• Ivrii, V. Ja. (1980), «The second term of the spectral asymptotics for a Laplace–Beltrami operator on manifolds with boundary», Funktsional. Anal. I Prilozhen 14 (2): 25-34, S2CID 123935462, doi:10.1007/BF01086550 . (En Russian).
• Kac, Mark (April 1966). «Can One Hear the Shape of a Drum?». American Mathematical Monthly 73 (4, part 2): 1-23. JSTOR 2313748. doi:10.2307/2313748. 
• Lapidus, Michel L. (1991), «Can One Hear the Shape of a Fractal Drum? Partial Resolution of the Weyl-Berry Conjecture», Geometric Analysis and Computer Graphics, Math. Sci. Res. Inst. Publ. 17 (17), New York: Springer, pp. 119-126, ISBN 978-1-4613-9713-7, doi:10.1007/978-1-4613-9711-3_13 .
• Lapidus, Michel L. (1993), «Vibrations of fractal drums, the Hipótesis de Riemann, waves in fractal media, and the Weyl–Berry conjecture», en B. D. Sleeman; R. J. Jarvis, eds., Ordinary and Partial Differential Equations, Vol IV, Proc. Twelfth Internat. Conf. (Dundee, Scotland, UK, June 1992), Pitman Research Notes in Math. Series 289, London: Longman and Technical, pp. 126-209 .
• Lapidus, M. L.; van Frankenhuysen, M. (2000), Fractal Geometry and Number Theory: Complex dimensions of fractal strings and zeros of zeta functions, Boston: Birkhauser .. (La segunda edición revisada y ampliada aparecerá en 2005.)
• Lapidus, Michel L.; Pomerance, Carl (1993), «The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums», Proc. London Math. Soc., Series 3 66 (1): 41-69, doi:10.1112/plms/s3-66.1.41, «citeseerx: 10.1.1.526.854» .
• Lapidus, Michel L.; Pomerance, Carl (1996), «Counterexamples to the modified Weyl–Berry conjecture on fractal drums», Math. Proc. Cambridge Philos. Soc. 119 (1): 167-178, Bibcode:1996MPCPS.119..167L, S2CID 33567484, doi:10.1017/S0305004100074053 .
• Milnor, John (1964), «Eigenvalues of the Laplace operator on certain manifolds», Proceedings of the National Academy of Sciences of the United States of America 51 (4): 542ff, Bibcode:1964PNAS...51..542M, PMC 300113, PMID 16591156, doi:10.1073/pnas.51.4.542 .
• Sunada, T. (1985), «Riemannian coverings and isospectral manifolds», Ann. of Math., 2 121 (1): 169-186, JSTOR 1971195, doi:10.2307/1971195 .
• Zelditch, S. (2000), «Spectral determination of analytic bi-axisymmetric plane domains», Geometric and Functional Analysis 10 (3): 628-677, S2CID 16324240, arXiv:math/9901005, doi:10.1007/PL00001633 .

• Simulación que muestra soluciones de la ecuación de onda en dos tambores isoespectrales
• Isospectral Drums de Toby Driscoll en la Universidad de Delaware
• Algunos dominios isoespectrales planos por Peter Buser, John Horton Conway, Peter Doyle y Klaus-Dieter Semmler
  • Representación 3D de la batería homofónica Buser-Conway-Doyle-Semmler
• Drums That Sound Alike de Ivars Peterson en el sitio web de la Mathematical Association of America
• Weisstein, Eric W. «Isospectral Manifolds». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Benguria, Rafael D. (2001), «Escuchar la forma de un tambor», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .