Produit zig-zag de graphes

Pour les articles homonymes, voir Zigzag (homonymie).
En théorie des graphes, le produit zig-zag de graphes est une opération sur des graphes réguliers. Le produit de deux graphes et , noté , prend en arguments un grand graphe et un petit graphe et produit un graphe qui hérite approximativement de la taille du grand graphe et du degré du petit. Une propriété importante du produit zig-zag est que si est un bon graphe expanseur, alors le taux d'expansion du graphe résultat est seulement un peu moins bon que le taux d'expansion de .
De manière informelle, le produit zig-zag [1] remplace chaque sommet de par une copie de (un « nuage », cloud en anglais) et relie les sommets en trois étapes : une première (le zig) à l'intérieur du nuage, suivi d'une deuxième entre deux nuages, et enfin une troisième (le zag) à l'intérieur du nuage d'arrivée.
Le produit zig-zag a été introduit par Omer Reingold, Salil Vadhan et Avi Wigderson en 2002[2] et a été utilisé pour la construction explicite d'expanseurs et d'extracteurs de degré constant. Les auteurs ont obtenu le prix Gödel pour ce travail[3]. Ultérieurement le produit zig-zag a été employé en théorie de complexité pour prouver que les classes de complexité SL (espace logarithmique symétrique) et L (espace logarithmique) coïncident[4].
Définitions
Les graphes considérés ici sont non orientés et réguliers. De plus, le degré du premier correspond au nombre de sommets du second.
Définition simplifiée
En suivant l'exposé des auteurs[2], on présente d'abord une version simplifiée de la définition du produit zig-zag. Dans cette définition, on se restreint aux graphes réguliers de degré qui possèdent une coloration des arêtes avec seulement couleurs[5]. Dans une telle coloration, deux arêtes incidentes en un même sommet sont toujours de couleur différente.
Soient un graphe -régulier (régulier de degré ) sur un ensemble de sommets et un graphe -régulier sur un ensemble de sommets. On note que l'entier est à la fois le degré de , le nombre de couleurs de et le nombre de sommets de : on colore de façon arbitraire les sommets de avec ces couleurs.
-
 Le graphe 4-régulier G à gauche et le graphe 1-régulier H à droite.
Le graphe 4-régulier G à gauche et le graphe 1-régulier H à droite. -
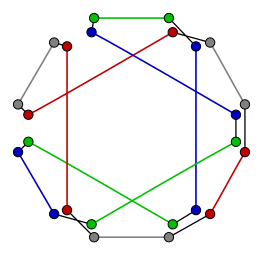 Après remplacement des sommets de G par des nuages issus de H.
Après remplacement des sommets de G par des nuages issus de H. -
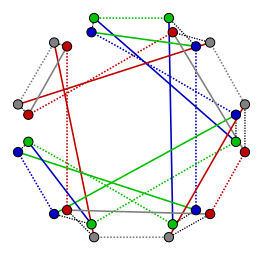 La procédure de remplacement des arêtes en zig-zag.
La procédure de remplacement des arêtes en zig-zag. -
 Le résultat final est 1-régulier.
Le résultat final est 1-régulier.
On procède ainsi pour obtenir le produit zig-zag des graphes et , noté [1] :
- Chaque sommet de est remplacé par une copie du graphe , son « nuage ».
- Deux sommets et dans le graphe résultant sont liés lorsqu'il existe deux sommets et tels que :
- et sont liés dans (le zig) ;
- et sont de même couleur et font partie de nuages issus de sommets qui sont liés dans ;
- et sont liés dans (le zag).
Le graphe résultant :
- possède sommets, puisqu'on remplace chacun des sommets de par sommets de ;
- est de degré , puisque, depuis un sommet donné, il y a possibilités pour le zig, une seule possibilité pour le trajet intermédiaire, et à nouveau possibilités pour le zag.
-
 Cette fois, H est un graphe 2-régulier.
Cette fois, H est un graphe 2-régulier. -
 Après remplacement des sommets.
Après remplacement des sommets. -
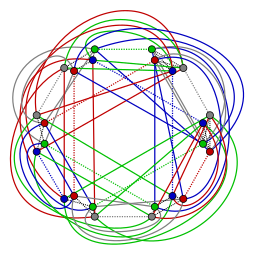 Le zig-zag.
Le zig-zag. -
 Le résultat final est cette fois 4-régulier.
Le résultat final est cette fois 4-régulier.
Application de rotation
Dans le cas général, on ne suppose pas qu'une coloration avec D couleurs existe.
On considère ici que les arêtes issues d'un sommet sont numérotées ; de plus, pour un graphe à sommets, on identifie ses sommets à l'ensemble des entiers de à , et on le note . Un couple d'entiers peut être employé pour désigner la e arête sortant du sommet .
Soit un graphe -régulier (régulier de degré ). L’application de rotation
est l'application définie comme suit :
si la e arête sortant de mène à et la e arête sortant de mène à , autrement dit si l'arête est la e arête sortant de et la e arête sortant de .
L'application de rotation remplace et généralise la coloration de la définition précédente. Si une coloration avec D couleurs existe, alors on peut s'arranger pour numéroter chaque sommet de telle façon que .
Il résulte de la définition que est une bijection, et de plus que est l'application identité. En d'autres termes, est une involution.
Définition du produit zig-zag

Soit un graphe -régulier sur l'ensemble de sommets et d'application de rotation , et soit un graphe -régulier sur l'ensemble de sommets et d'application de rotation .
Le produit zig-zag est le graphe -régulier dont l'ensemble des sommets est et dont l'application de rotation est définie par
où sont construits successivement en posant
- , le zig
- ,
- , le zag.
Les sommets du graphe sont des couples de . Les arêtes de ce graphe portent des couples d'étiquettes du graphe -régulier, correspondant aux deux décisions à prendre en partant d'un sommet donné.
Ici encore, le graphe produit comporte sommets et est -régulier.
Propriétés
Réduction du degré
Par définition, le produit zig-zag transforme un graphe -régulier en un nouveau graphe qui est -régulier. Ainsi, si le degré de est nettement plus grand que celui de , le produit zig-zag réduit le degré de .
Préservation du trou spectral
Le taux d'expansion d'un graphe peut être mesuré par son trou spectral, qui est la différence entre la plus grande et la deuxième plus grande valeur propre de sa matrice d'adjacence. Une propriété importante du produit zig-zag est qu'il préserve le trou spectral, en ce sens que si est un graphe expanseur « assez bon » (avec un grand trou spectral), alors le taux d'expansion du produit zig-zag est proche de celui du graphe original .
Formellement, appelons graphe de type un graphe -régulier sur sommets dont la deuxième valeur propre est majorée en valeur absolue par . Soient et des graphes de type et respectivement. Alors est de type
- ,
avec .
Préservation de la connexité
Le produit zig-zag opère séparément sur chaque composante connexe de . Plus formellement, soient un graphe -régulier sur l'ensemble de sommets et un graphe -régulier sur l'ensemble de sommets. Si est une composante connexe de , alors on a , où est le sous-graphe de induit par (c'est-à-dire le graphe sur qui contient les arêtes de dont les deux extrémités sont dans ).
Applications
Construction d'un expanseur de degré constant
Dans leur article de 2002[2], Reingold, Vadhan, et Wigderson donnent une construction combinatoire explicite et simple de graphes expanseurs de degré constant. La construction est itérative. La bloc de base est un expanseur unique de taille fixe. À chaque itération, le produit zig-zag sert à construire un autre graphe dont la taille augmente, mais dont le degré et le taux d'expansion restent inchangés. Ce processus peut être répété et donne des expanseurs de taille arbitrairement grande.
Solution du problème de connexité en espace logarithmique
En 2008[4], Reingold présente un algorithme qui résout le problème dit de la st-connexité en espace logarithmique. Il s'agit du problème de déterminer si, dans un graphe non orienté, deux sommets s et t donnés sont dans la même composante connexe. L'algorithme repose de manière essentielle sur le produit zig-zag.
De manière informelle, pour résoudre le problème de la st-connexité en espace logarithmique, le graphe d'entrée est transformé, en utilisant une combinaison d'exponentiations et de produits zig-zag, en un graphe régulier de degré constant avec un diamètre logarithmique. L'élévation à la puissance accroît le taux d'expansion (et donc réduit le diamètre) au prix de l'accroissement du degré, et le produit zig-zag est utilisé pour réduire le degré tout en préservant le taux d'expansion.
Voir aussi
Bibliographie
- Omer Reingold, Luca Trevisan et Salil Vadhan, « Pseudorandom walks on regular digraphs and the RL vs. L problem », dans Proc. 38th ACM Symposium on Theory of Computing Proc. (STOC), (DOI 10.1145/1132516.1132583), p. 457–466.
Articles connexes
Notes et références
- (en) Cet article est partiellement ou en totalité issu des articles intitulés en anglais « zig-zag product » (voir la liste des auteurs) et « rotation map » (voir la liste des auteurs).
- ↑ a et b Les auteurs utilisent une notation plus compliquée que l'on ne peut pas reproduire dans le Latex disponible sur Wikipédia.
- ↑ a b et c Omer Reingold, Salil Vadhan et Avi Wigderson, « Entropy waves, the zig-zag graph product, and new constant-degree expanders », Annals of Mathematics, vol. 155, no 1, , p. 157–187 (DOI 10.2307/3062153, JSTOR 3062153, MR 1888797).
- ↑ Page du prix Gödel 2009.
- ↑ a et b Omer Reingold, « Undirected connectivity in log-space », Journal of the ACM, vol. 55, no 4, , p. 1–24 (DOI 10.1145/1391289.1391291).
- ↑ Cela exclut par exemple les graphes cycles dont le nombre de sommets est impair, qui sont 2-réguliers mais nécessitent 3 couleurs.
 Portail des mathématiques
Portail des mathématiques  Portail de l'informatique théorique
Portail de l'informatique théorique





















![{\displaystyle [N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82c5c29e2a04165395b2e0896d9425fd0039fc8b)


![{\displaystyle \mathrm {Rot} _{G}:[N]\times [D]\to [N]\times [D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9394e73894d527b3a1c1f789e084de853bb417df)


![{\displaystyle [v,w]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81599dd26b00c77086bda71448f9011328e690f1)



![{\displaystyle [D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c4bcb25d77a0de74082c849178200b8cf1340b4)

![{\displaystyle [N]\times [D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d759568406aafdda0ad85256796821fa996659e)

















![{\displaystyle S\subseteq [N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81b15bbb524309b0a13867fef77b414e3abab630)















