Norma (matematika)

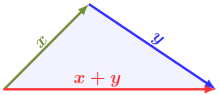
A norma olyan vektortéren vagy függvénytéren értelmezett ${\displaystyle d}$ leképezés, ami a nullvektor kivételével a tér minden vektorához egy pozitív számot rendel. Érvényesek rá a következő, az abszolút értékhez hasonló tulajdonságok:

• ${\displaystyle d(\mathbf {x} )\geq 0}$
• ${\displaystyle d(\mathbf {x} )=0}$ akkor és csak akkor, ha ${\displaystyle \mathbf {x} =\mathbf {0} }$
• ${\displaystyle d(\mathbf {x} +\mathbf {y} )\leq d(\mathbf {x} )+d(\mathbf {y} )}$
• ${\displaystyle d(\lambda \mathbf {x} )=\left\vert \lambda \right\vert d(\mathbf {x} )}$

${\displaystyle d(\mathbf {x} )}$-et az ${\displaystyle \mathbf {x} }$ normájának nevezzük.

A normát valós vagy komplex vektor- vagy függvénytéren vezetik be. A normával ellátott tereket normált tereknek hívják. A fogalom bevezetésének motivációja a „hosszúság” fogalmának kezelése absztrakt terekben. A normált terek több fontos analitikus tulajdonsággal bírnak, mivel a norma metrikát, és ezzel topológiát indukál. Ekvivalens normák ugyanazt a topológiát indukálják. Ha egy térten skalárszorzat van értelmezve, akkor az normát indukál. Véges dimenziós vektorterekben minden norma ekvivalens.^[1]

A norma definícióját Stefan Banach vezette be 1922-ben disszertációjában.^[2][3] A ma használt norma szimbólumot Erhard Schmidt alkalmazta először 1908-ban a vektorok közötti távolságra.^[4]

Egy ${\displaystyle z\in \mathbb {R} }$ szám abszolútértéke egy egyszerű példa a normára. Az abszolútérték az előjel elhagyásával kapható, azaz

${\displaystyle \|z\|=|z|={\sqrt {z^{2}}}={\begin{cases}\,\ \ z&\mathrm {ha} \ z\geq 0\\\,-z&\mathrm {ha} \ z<0.\end{cases}}}$

Egy ${\displaystyle z\in \mathbb {C} }$ komplex szám abszolútértéke

${\displaystyle \|z\|=|z|={\sqrt {z{\bar {z}}}}={\sqrt {\left(\operatorname {Re} z\right)^{2}+\left(\operatorname {Im} z\right)^{2}}}}$

ahol ${\displaystyle {\bar {z}}}$ a ${\displaystyle z}$ szám komplex konjugáltja, ${\displaystyle \operatorname {Re} }$ a valós része és ${\displaystyle \operatorname {Im} }$ a képzetes része. Egy komplex szám abszolútértéke megfelel a vektorának a hosszának a Gauß-féle számsíkon.

Az abszolútérték-normát két valós, illetve komplex szám skalárszorzata indukálja:

${\displaystyle \langle w,z\rangle =w\cdot z}$   ha   ${\displaystyle w,z\in \mathbb {R} }$    illetve    ${\displaystyle \langle w,z\rangle =w\cdot {\bar {z}}}$   ha   ${\displaystyle w,z\in \mathbb {C} }$

Véges dimenzióban minden norma ekvivalens, azaz ugyanazok a sorozatok konvergensek minden normában.

Egy szabványos példa az euklideszi norma. Például az ${\displaystyle \mathbb {R} ^{2}}$ síkban az ${\displaystyle (x,y)}$ vektor normája:

${\displaystyle \|(x,y)\|={\sqrt {x^{2}+y^{2}}}}$,

ami megfelel a szokásos, Pitagorasz-tétellel számítható vektorhosszúságnak.

Az n dimenziós valós (és komplex) vektortereken többnyire a p-normákat (Hölder-normák) használják:

${\displaystyle \|x\|_{p}:=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}}$

A ${\displaystyle p}$-normák egységgömbjei két dimenzióban szub- illetve szuperellipszisek alakját öltik. Három dimenzióban szub-, illetve szuperellipszoidok.

A ${\displaystyle p}$-normák teljesítik a Minkowski-egyenlőtlenséget és a Hölder-egyenlőtlenséget. Növekvő ${\displaystyle p}$-re monoton csökkennek. A határoló tényezők ${\displaystyle 1\leq p\leq r\leq \infty }$ esetén:

${\displaystyle \|x\|_{r}\leq \|x\|_{p}\leq n^{{\frac {1}{p}}-{\frac {1}{r}}}\|x\|_{r}}$,

ahol a maximumnorma esetén a ${\displaystyle {\tfrac {1}{\infty }}=0}$ helyettesítést kell végezni. Így a ${\displaystyle p}$-normák egymástól legfeljebb egy ${\displaystyle n}$-es tényezőben különbözhetnek.

Az analóg módon ${\displaystyle p<1}$ tényezővel számolt mennyiségek megsértik a háromszög-egyenlőtlenséget, a belőlük számított gömb konkáv.

Különösen gyakran fordulnak elő az 1-es, a 2-es és a végtelen-normák.

Az 1-norma: ${\displaystyle \|x\|_{1}=\sum _{i=1}^{n}|x_{i}|}$.

Két dimenzióban a normagömb négyzet, három dimenzióban oktaéder, magasabb dimenzióban keresztpolitóp.

A belőle származó távolságot nevezik Manhattan-metrikának vagy taximetrikának, mivel olyan utak mentén méri a távolságokat, amelyek nem mehetnek ferdén, azaz minden szakaszuk párhuzamos a koordinátatengelyekkel. Például ${\displaystyle \mathbb {R} ^{2}}$-ben a szakaszok csak vízszintesek és függőlegesek lehetnek.

A 2-norma: ${\displaystyle \|x\|_{2}={\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}}$

Skalárszorzatból származik. Ez azt jelenti, hogy van egy ${\displaystyle \langle \cdot ,\cdot \rangle }$ skalárszorzat, amivel teljesül, hogy ${\displaystyle \|x\|:={\sqrt {\langle x,x\rangle }}}$, valamint teljesül rá a Pitagorasz-tétel, a paralelogrammaszabály, és komplex terekben a polarizációs egyenlőség.

A többi normához nincs ilyen skalárszorzat: a paralelogrammaszabállyal egyetlen jelölt adódik. A skalárszorzat tulajdonságait ellenőrizve kiderül, hogy nem teljesíti ezeket a tulajdonságokat.

Két dimenzióban a normagömb kör, három dimenzióban gömb, magasabb dimenzióban hipergömb. Két és három dimenzióban a szokásos vektorhossznak felel meg. Unitér transzformációk, például az origó körüli forgatások egyedüliként ezt a normát őrzik meg. Az euklideszi normával ellátott vektortereket euklideszi vektortereknek nevezik. Belőle származik az euklideszi metrika, ahol a távolságok Pitagorasz-tétellel számíthatók.

Értelmeznek ${\displaystyle \infty }$-normát is, ahol ${\displaystyle \|x\|_{\infty }=\max _{i=1}^{n}|x_{i}|}$

Határértékként is megkapható a p-normákból, ahol p tart a végtelenbe. Nevezik Csebisev-normának is. Két dimenzióban a normagömb négyzet, három dimenzióban kocka, magasabb dimenzióban hiperkocka.

A belőle származó metrikát nevezik maximummetrikának, Csebisev-metrikának vagy német szaknyelvben sakktáblametrikának is, ugyanis szemléletesen azoknak a lépéseknek a számát jelenti, ahány lépéssel az egyik pontból egy királlyal egy másik pontba lehet eljutni. Ennek során a király átlósan is léphet.

Az ${\displaystyle n}$ dimenziós maximumnorma előáll szorzatnormaként a ${\displaystyle V=V_{1}\times \dotsb \times V_{n}}$ téren, ahol ${\displaystyle (V_{i},\|\cdot \|_{i})}$ vektorterek, ${\displaystyle x=(x_{1},\dotsc ,x_{n})}$ és ${\displaystyle x_{i}\in V_{i}}$.

Mátrixnormák esetén gyakran megkövetelik még a szubmulitiplikativitást:

${\displaystyle \|A\cdot B\|\leq \|A\|\cdot \|B\|}$

Ha egy mátrixnorma szubmultiplikatív, akkor a mátrix spektrálrádiusza (a legnagyobb abszolútértékű sajátérték abszolútértéke) nem nagyobb, mint a norma. Vannak azonban olyan mátrixnormák, melyek teljesítik a szokásos normatulajdonságokat, de nem szubmultiplikatívak. Egy mátrixnorma kompatibilis egy vektornormával, ha

${\displaystyle \|A\cdot x\|\leq \|A\|\cdot \|x\|}$

minden ${\displaystyle x\in {\mathbb {K} }^{n}}$ esetén.

A vektornormák mátrixnormákat indukálnak:

${\displaystyle \|A\|_{M}=\sup _{x\not =0}{\frac {\|Ax\|_{V}}{\|x\|_{V}}}=\sup _{\|x\|_{V}=1}\|Ax\|_{V}}$

Itt a sup helyett maximum is írható. A linearitás folytán elég az 1 normájú vektorokat tekinteni, és mivel ez kompakt halmaz, a folytonos ${\displaystyle \|Ax\|_{V}}$ függvény felveszi a maximumát. Ez az a maximális érték, amivel a mátrix megnyújt egy vektort. Kompatibilis azzal a vektornormával, amiből származik.

Az indukált mátrixnormákra teljesül:

• ${\displaystyle \lVert A\cdot B\rVert \leq \lVert A\rVert \cdot \lVert B\rVert }$
• ${\displaystyle \lVert A\mathbf {x} \rVert _{V}\leq \lVert A\rVert _{M}\cdot \lVert \mathbf {x} \rVert _{V}}$

Többnyire itt is az 1-es, a 2-es és a végtelen normát használják.

• Az 1-es norma által indukált mátrixnorma az oszlopösszegnorma, vagy röviden oszlopnorma:

${\displaystyle \left\|A\right\|_{1}=\max _{j}{\sum _{i=1}^{m}\left|a_{ij}\right|}}$

• A végtelen norma a sorösszegnormát, más néven a sornormát indukálja:

${\displaystyle \left\|A\right\|_{\infty }=\max _{i}{\sum _{j=1}^{n}\left|a_{ij}\right|}}$

• A 2-es norma indukálta mátrixnorma:

${\displaystyle \left\|A\right\|_{2}={\sqrt {\lambda _{\rm {max}}(A^{H}A)}}=\sigma _{\text{max}}(A)}$, azaz a mátrix legnagyobb szinguláris értéke. A képletben ${\displaystyle A^{H}}$ a mátrix konjugált transzponáltja, és ${\displaystyle \lambda _{\rm {max}}}$ az ${\displaystyle A^{H}A}$ szorzatmátrix abszolút értékben legnagyobb sajátértéke.

Ezek a vektornormák úgy állnak elő, hogy a mátrixot vektorként tekintjük, és alkalmazzuk rá az adott vektornormát. Például a Frobenius-norma a 2-es normából áll elő: ${\displaystyle m\times n}$-es A mátrixra:

${\displaystyle \|A\|_{F}^{2}=\sum _{i=1}^{m}\sum _{j=1}^{n}|a_{ij}|^{2}.}$

A maximumnormára az összegnorma alapul. Mindkettő szubmultiplikatív, és kompatibilis az euklideszi normával.

Egy további lehetőség, ha tekintjük a mátrix szinguláris érték felbontását, azaz az ${\displaystyle A=U\Sigma V^{H}}$ előállítást, ahol ${\displaystyle U}$ unitér, ${\displaystyle \Sigma }$ diagonális, ${\displaystyle V^{H}}$ pedig adjungált unitér. Ekkor a ${\displaystyle \Sigma }$ mátrix átlóján szereplő ${\displaystyle \sigma _{1},\ldots ,\sigma _{r}}$ értékek nemnegatív valós számok, és az ${\displaystyle A}$ mátrix szinguláris értékeinek nevezzük őket. Megegyeznek az ${\displaystyle A^{H}A}$ mátrix sajátértékeinek négyzetgyökeivel. A ${\displaystyle \sigma =(\sigma _{1},\ldots ,\sigma _{r})}$ szinguláris értékeket betesszük egy vektorba, és ennek vesszük valamelyik normáját, tehát

${\displaystyle \|A\|=\|\sigma \|}$.

Erre a típusra példák az árnyéknormák, melyek a szinguláris értékekből alkotott vektor ${\displaystyle p}$-normái, illetve a Ky–Fan-normák, melyek a legnagyobb szinguláris értékek összegén alapulnak. Nevezetesen, a ${\displaystyle k}$-adik Ky–Fan-norma a legnagyobb ${\displaystyle k}$ szinguláris érték összege.

Ha sorozatok normájáról esik szó, akkor csak valós vagy komplex elemekből álló sorozatokat tekintenek, ahol ${\displaystyle (a_{n})_{n}=(a_{1},a_{2},\ldots )\in {\mathbb {K} }^{\mathbb {N} }}$ és ${\displaystyle a_{n}\in {\mathbb {K} }}$ minden ${\displaystyle n\in \mathbb {N} }$ esetén. Ezzel a sorozatok a véges dimenziós vektorok általánosításai. Mivel a sorozatokban végtelen sok nullától különböző elem lehet, azért a vektornormák nem vihetők át közvetlenül a sorozatokra. Például lehet, hogy nincs maximális abszolútértékű tag vagy az összes tag összege nem konvergens. Hasonlóan nincs biztosítva a tagok négyzetéből képzett sor konvergenciája. Éppen ezért a normákat rendszerint nem az összes valós vagy komplex sorozatra vezetik be, hanem alkalmas alterekre.

Az ${\displaystyle \ell ^{p}}$-terek azokból a sorozatokból állnak, amelyekben a tagok abszolút értékes p-edik hatványának összege konvergens.

${\displaystyle \ell ^{p}:=\left\{\left(a_{n}\right)\in \mathbb {K} ^{\mathbb {N} }\colon \left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)<\infty \right\},\qquad p\in [1,\infty )}$

és ${\displaystyle \ell ^{\infty }:=\left\{(a_{n})\in \mathbb {K} ^{\mathbb {N} }\colon \sup _{n\in \mathbb {N} }|a_{n}|<\infty \right\}}$

A véges dimenziós esethez hasonlóan értelmezik a p-normákat:

${\displaystyle \|(a_{n})\|_{p}:={\sqrt[{p}]{\sum _{n=0}^{\infty }|a_{n}|^{p}}}}$ p véges

és ${\displaystyle \|(a_{n})\|_{\infty }:=\sup _{n\in \mathbb {N} }|a_{n}|}$ p végtelen, ami a szuprémumnorma korlátos sorozatokra.

Az ${\displaystyle \ell ^{p}}$-terek az ${\displaystyle \ell ^{p}}$-normákkal ellátva teljes normált terek.^[5] Az ${\displaystyle \ell ^{2}}$-tér Hilbert-tér, az ${\displaystyle \left\langle \,(a_{n}),(b_{n})\,\right\rangle _{\ell ^{2}}=\sum _{n=1}^{\infty }a_{n}\cdot {\overline {b_{n}}}}$ skalárszorzattal.

A korlátos sorozatok tere, ${\displaystyle \ell ^{\infty }}$; a konvergens sorozatok tere, ${\displaystyle c}$; és a nullához tartó sorozatok (nullsorozatok) tere, ${\displaystyle c_{0}}$ a szuprémumnormával ellátva teljes normált terek.^[5] Egy ${\displaystyle \ell ^{p}}$-norma duális normája egy ${\displaystyle \ell ^{q}}$ norma, ahol ${\displaystyle (1/p)+(1/q)=1}$, ha ${\displaystyle 1\leq p<\infty }$. Az ${\displaystyle \ell ^{1}}$ térnek nem az ${\displaystyle \ell ^{\infty }}$ tér a duálisa, hanem a konvergens sorozatok tere és a nullsorozatok tere a szuprémumnormával.

Egy korlátos változású sorozat ${\displaystyle bv}$-normája:

${\displaystyle \|(a_{n})\|_{bv}=|a_{1}|+\sum _{n=1}^{\infty }|a_{n+1}-a_{n}|}$.

A ${\displaystyle bv}$-normával a korlátos változású sorozatok ${\displaystyle bv}$ tere teljes normált tér, mivel minden korlátos változású sorozat Cauchy-sorozat is. A korlátos változású nullsorozatok ${\displaystyle bv_{0}}$ terén értelmezhető a ${\displaystyle bv_{0}}$-norma az első tag elhagyásával:

${\displaystyle \|(a_{n})\|_{bv_{0}}=\sum _{n=1}^{\infty }|a_{n+1}-a_{n}|}$,

amely normával a ${\displaystyle bv_{0}}$ tér teljes.

A következőkben egy adott ${\displaystyle \Omega }$ halmazon értelmezett valós, illetve komplex értékű ${\displaystyle f\colon \Omega \rightarrow {\mathbb {K} }}$ függvényeket tekintünk. Az ${\displaystyle \Omega }$ halmaz gyakran topologikus tér, hogy lehessen folytonosságról beszélni. Sok alkalmazásban ${\displaystyle \Omega }$ az ${\displaystyle \mathbb {R} ^{n}}$ részhalmaza. A sorozatokhoz hasonlóan a függvények is lehetnek végtelenek, így szintén nem értelmezünk normákat az összes függvényre. A legfontosabb alterek a korlátos, folytonos, integrálható vagy differenciálható függvények tere. Általánosabban Banach-terekbe is képezhetnek a függvények, ahol az abszolútérték szerepét a Banach-tér normája veszi át.

Az L^p-terek azokat a függvényeket tartalmazzák, amiknek a p-edik hatványa integrálható. Ha ezekre a függvényekre vesszük az analóg leképezést:

${\displaystyle \|f\|_{p}:=\left(\int _{\Omega }\|f(x)\|^{p}\,d\mu (x)\right)^{1/p}}$,

akkor egy úgynevezett félnormát kapunk, mert ez az integrál nemcsak az azonosan nulla függvényre nulla, hanem azokra is, amik majdnem mindenhol nullát vesznek fel. Tekintsük ekvivalensnek azokat a függvényeket, amik majdnem mindenütt egyenlők. Ezeken az ekvivalenciaosztályokon ez az integrál norma. A Fischer–Riesz-tétel miatt az ${\displaystyle L^{p}}$-normával az ${\displaystyle L^{p}}$-terek teljes normált terek. Az ${\displaystyle L^{1}(\Omega )}$ tér a Lebesgue-integrálható függvények ekvivalenciaosztályainak tere.

Többnyire itt is az 1-es, a 2-es és a határértékként kapható végtelen normát használják, bár előfordulnak fizikai példák más p-kre, mint a hősugárzási egyenlet megoldása az L⁵-térben.

A 2-es norma skalárszorzatból származik. Ez azt jelenti, hogy van egy ${\displaystyle \langle \cdot ,\cdot \rangle }$ skalárszorzat, amivel teljesül, hogy: ${\displaystyle \|x\|:={\sqrt {\langle x,x\rangle }}}$. Valamint teljesül rá a Pitagorasz-tétel, a paralelogrammaszabály, és komplex terekben a polarizációs egyenlőség. Ez a skalárszorzat

${\displaystyle \langle f,g\rangle _{L_{2}(\Omega )}=\int _{\Omega }f(x)\cdot {\overline {g(x)}}\,dx}$

amivel az ${\displaystyle L^{2}(\Omega )}$ tér Hilbert-tér.

A többi normához nincs ilyen skalárszorzat: a paralelogrammaszabállyal egyetlen jelölt adódik. A skalárszorzat tulajdonságait ellenőrizve kiderül, hogy nem teljesíti ezeket a tulajdonságokat.

Az ${\displaystyle p\rightarrow \infty }$ határértékeként adódik a lényegében korlátos függvények ${\displaystyle L^{\infty }(\Omega )}$ tere. Az ${\displaystyle 1\leq p<\infty }$ esetben az ${\displaystyle L^{p}}$-normával duális norma az ${\displaystyle L^{q}}$-norma, ahol ${\displaystyle (1/p)+(1/q)=1}$. Az ${\displaystyle L^{p}}$-normák és terek a Lebesgue-mértékkel kiterjeszthetők mértékké, ahol a dualitás ${\displaystyle p=1}$ esetén csak bizonyos mértékterekben teljesül.^[6]

A szuprémumnorma korlátos függvényeken értelmezett, ahol korlátos az a függvény, melynek képe ${\displaystyle \mathbb {K} }$ korlátos részhalmaza, definíció szerint

${\displaystyle \|f\|_{B(\Omega )}=\|f\|_{\infty }=\|f\|_{\sup }=\sup _{x\in \Omega }|f(x)|}$.

A korlátos függvények halmaza a szuprémumnormával teljes normált tér.^[7]

Kompakt halmazon értelmezett folytonos függvény maximumnormája:

${\displaystyle \|f\|_{C^{0}(\Omega )}=\|f\|_{\infty }=\|f\|_{\max }=\max _{x\in \Omega }|f(x)|}$.

A Weierstrass-szélsőértéktétel miatt kompakt halmazon értelmezett folytonos függvény felveszi a szuprémumát. Egy adott kompakt halmazon értelmezett folytonos függvények tere teljes normált teret alkot a maximumnormával.^[8]

Egy ${\displaystyle (\Omega ,{\mathcal {X}},\mu )}$ mértéktéren majdnem mindenütt korlátos függvény ${\displaystyle {\mathcal {L}}^{\infty }}$-normája

${\displaystyle \|f\|_{{\mathcal {L}}^{\infty }(\Omega )}=\operatorname {ess\;} \sup _{x\in \Omega }|f(x)|=\inf _{N\subset \Omega \atop \mu (N)=0}\;\sup _{x\in \Omega \setminus N}|f(x)|}$,

ahol ${\displaystyle N}$ nullhalmaz, tehát a ${\displaystyle {\mathcal {X}}}$ σ-algebra egy eleme, aminek a mértéke a ${\displaystyle \mu }$ mérték szerint nulla. Egy majdnem mindenütt korlátos függvény néhány ${\displaystyle {x\in N}}$ pontban abszolútértékben nagyobb értéket is felvehet, mint a lényegi szuprémuma. Általában a lényegi szuprémum csak félnorma, mivel nemcsak az azonosan nulla függvény lényegi szuprémuma nulla, hanem például azoké a függvényeké is, amelyek véges sok pontban különböznek tőle. Tehát inkább azoknak a ${\displaystyle f\in {\mathcal {L}}^{\infty }(\Omega )}$-beli függvényeknek az az ${\displaystyle [f]}$ halmazait tekintjük, amelyek majdnem mindenütt egyenlőek, és a kapott faktorteret ${\displaystyle L^{\infty }(\Omega )}$-nek nevezzük. Ezen a téren a lényegi szuprémumnorma, definiálva, mint

${\displaystyle \|\,[f]\,\|_{L^{\infty }(\Omega )}=\|f\|_{{\mathcal {L}}^{\infty }(\Omega )}}$

valóban norma, ahol a jobb oldali érték független az ${\displaystyle f}$ reprezentáns választásától. Gyakran ${\displaystyle [f]\in L^{\infty }(\Omega )}$ helyett pontatlanul ${\displaystyle f\in L^{\infty }(\Omega )}$-t írnak. A lényegében korlátos függvények ekvivalenciaosztályainak ${\displaystyle L^{\infty }(\Omega )}$ tere a lényegi szuprémumnormával teljes normált tér.^[9]

Egy ${\displaystyle [a,b]}$ intervallumon értelmezett egydimenziós korlátos változású függvény ${\displaystyle BV}$-normáját a sorozatok ${\displaystyle bv}$-normájával analóg módon definiálják:

${\displaystyle \|f\|_{BV([a,b])}=|f(a)|+\sup _{P}\sum _{i=1}^{n}|f(x_{i})-f(x_{i-1})|}$,

ahol ${\displaystyle P=\{a=x_{0}<x_{1}<\ldots <x_{n}=b\}}$ az ${\displaystyle [a,b]}$ intervallum partíciója, és a szuprémum az összes partíciót tekintetbe veszi.^[10] Egy függvény pontosan korlátos változású, hogyha előáll két monoton növő függvény különbségeként.^[11] A korlátos változású függvények tere a ${\displaystyle BV}$-normával ellátva teljes normált tér. Alternatívan a normáláshoz ${\displaystyle |f(a)|}$ helyett a függvény teljes intervallumra vett integrálja is használható.^[12] A ${\displaystyle BV}$-norma és a hozzá tartozó függvényterek többféle általánosítása is létezik, így például a Fréchet-variáció, a Vitali-variáció és a Hardy-variáció.

Egy ${\displaystyle 0<\alpha \leq 1}$ kitevővel Hölder-folytonos függvény Hölder-normája

${\displaystyle \|f\|_{C^{0,\alpha }(\Omega )}=\|f\|_{C^{0}(\Omega )}+\operatorname {Hol} _{\alpha }(f,\Omega )}$,

ahol a függvény Hölder-konstansa

${\displaystyle \operatorname {Hol} _{\alpha }(f,\Omega )=\sup _{{x,y\in \Omega } \atop {x\neq y}}{\frac {|f(x)-f(y)|}{|x-y|^{\alpha }}}}$

A Hölder-konstans a folytonossági modulus egy speciális fajtája, és önmagában félnorma. A Hölder-folytonos függvények terei a megfelelő Hölder-normával teljes normált terek. Speciálisan, ha ${\displaystyle \alpha =1}$, akkor Lipschitz-folytonos függvényekről, Lipschitz-konstansról és Lipschitz-normáról van szó.^[13]

A ${\displaystyle C^{m}}$-normákat ezekre a függvényekre értelmezzük: Egy ${\displaystyle \Omega }$ nyílt halmazon ${\displaystyle m}$-szer folytonosan differenciálható függvények, melyek parciális deriváltjai az ${\displaystyle {\bar {\Omega }}}$ halmazra folytonosan kiterjeszthetők, éspedig úgy, hogy:

${\displaystyle \|f\|_{C^{m}({\bar {\Omega }})}=\max _{|s|\leq m}\;\|\partial ^{s}f\|_{C^{0}({\bar {\Omega }})}}$,

ahol ${\displaystyle s=(s_{1},\ldots ,s_{n})}$ nemnegatív egész számokból alkotott multiindex, ${\displaystyle \partial ^{s}f}$ az adott multiindexhez tartozó parciális derivált, és ${\displaystyle |s|=s_{1}+\ldots +s_{n}}$ a derivált rendje. Ezzel a ${\displaystyle C^{0}}$-norma megegyezik a szuprémumnormával és a ${\displaystyle C^{1}}$-norma a függvény és első deriváltjainak maximumával. A ${\displaystyle C^{m}({\bar {\Omega }})}$-terek a megfelelő ${\displaystyle C^{m}}$-normával teljes normált terek. Alternatívan, a ${\displaystyle C^{m}}$-normákat a maximumok helyett az összegükkel definiálják, azonban ez a két norma ekvivalens.^[14]

Ezzel analóg módon értelmezzük a ${\displaystyle C^{m,\alpha }}$-normát a nyílt halmazon ${\displaystyle m}$-szer folytonosan differenciálható függvényekre, melyek vegyes parciális deriváltjai folytonosan kiterjeszthetők a nyílt halmaz lezártjára, és melyek Hölder-konstansai ${\displaystyle m}$-ig korlátosak, ${\displaystyle f\in C^{m,\alpha }({\bar {\Omega }})}$, éspedig úgy, mint:

${\displaystyle \|f\|_{C^{m,\alpha }}({\bar {\Omega }})=\sum _{|s|\leq m}\|\partial ^{s}f\|_{C^{0}({\bar {\Omega }})}+\sum _{|s|=m}\operatorname {Hol} _{\alpha }(\partial ^{s}f,{\bar {\Omega }})}$.

Ezek a Hölder-folytonosan differenciálható függvények a ${\displaystyle C^{m,\alpha }}$-normával teljes normált teret alkotnak.^[15]

A Szoboljev-normákat a következőképpen értelmezik: Nyílt halmazokon értelmezett ${\displaystyle m}$-szer gyengén differenciálható függvények, melyek ${\displaystyle \partial ^{s}f}$ gyenge parciális deriváltjai ${\displaystyle m}$-edfokig ${\displaystyle p}$-edik hatványukban Lebesgue-integrálhatók, illetve ${\displaystyle 1\leq p<\infty }$, ekképpen:

${\displaystyle \|f\|_{W^{m,p}(\Omega )}=\left(\sum _{|s|\leq m}\|\partial ^{s}f\|_{L^{p}(\Omega )}^{p}\right)^{1/p}}$

illetve ${\displaystyle p=\infty }$ esetén:

${\displaystyle \|f\|_{W^{m,\infty }(\Omega )}=\max _{|s|\leq m}\,\|\partial ^{s}f\|_{L^{\infty }(\Omega )}}$.

Ha az ${\displaystyle |s|=m}$-edrendű vegyes deriváltak összegét tekintjük, akkor félnormát kapunk, ami az ${\displaystyle m}$-edfokúaknál kisebb fokú polinomokon eltűnik. Szoboljev-térnek, jelben ${\displaystyle W^{m,p}(\Omega )}$-nak nevezzük azoknak a függvényeknek a halmazát, melyek legfeljebb ${\displaystyle m}$-edfokú vegyes gyenge deriváltjai ${\displaystyle L^{p}(\Omega )}$-beliek. A Szoboljev-terek a megfelelő Szoboljev-normával teljes normált teret alkotnak. Az ${\displaystyle W^{m,2}(\Omega )}$ terek Hilbert-terek az

${\displaystyle \langle f,g\rangle _{W^{m,2}(\Omega )}=\sum _{|s|\leq m}\int _{\Omega }\partial ^{s}f(x)\cdot {\overline {\partial ^{s}g(x)}}\,dx}$

skalárszorzattal. A Szoboljev-terek fontos szerepet játszanak a parciális differenciálegyenletek megoldáselméletében, mint a differenciáloperátorok természetes értelmezési tartományai, vagy a végeselem-módszer hibabecslései parciális differenciálegyenletek diszkretizálásánál.^[16]

A következőkben két normált vektortér közötti lineáris operátorokat tekintünk.

Az operátornormákat a mátrixnormákkal analóg módon definiálják:

${\displaystyle \|f\|=\sup _{x\in V\setminus \{0\}}{\frac {\|f(x)\|_{W}}{\|x\|_{V}}}=\sup _{\|x\|_{V}=1}\|f(x)\|_{W}}$.

Legyen ${\displaystyle g:X\rightarrow V}$ egy másik lineáris operátor. Ekkor teljesül:

${\displaystyle \|f\circ g\|\leq \|f\|\|g\|}$.

Véges dimenzióban automatikusan véges lesz a norma, és visszakapjuk a megfelelő mátrixnormát. Ez a függvényterekben már nem igaz, a norma végtelen is lehet, például a differenciáloperátorok esetében. Szigorúan véve nem lesz norma a fenti értelemben.

Be lehet bizonyítani, hogy egy operátor normája véges akkor és csak akkor, ha folytonos. Egy adott teljes normált térbe képező folytonos operátorok tere teljes. Az operátornormák mindig szubmultiplikatívak, ugyanis ha a két tér megegyezik és teljes, akkor a folytonos lineáris operátorok tere az operátornormával és a kompozícióval Banach-algebrát alkot.^[17]

Két Banach-tér közötti ${\displaystyle T:V\rightarrow W}$ nukleáris operátor normáját a következőképpen definiálják:

${\displaystyle \|T\|_{1}=\inf \sum _{i=1}^{\infty }\|x'_{i}\|_{V'}\|y_{i}\|_{W}}$,

ahol ${\displaystyle (x'_{i})_{i}}$ egy ${\displaystyle V'}$ duális térbeli vektorsorozat, és ${\displaystyle (y_{i})_{i}}$ egy ${\displaystyle W}$-beli vektorokból álló sorozat. Így ${\displaystyle T}$ írható úgy, mint ${\displaystyle \textstyle T(x)=\sum _{i=1}^{\infty }x'_{i}(x)y_{i}}$, és ezeknek a nukleáris ábrázolásoknak az infimumát tekintjük. Ha mindkét vektortér Hilbert, akkor a megfelelő nukleáris norma a nyomnorma. A nukleáris operátorok tere a nukleáris normával teljes normált tér.^[18]

Egy Hilbert–Schmidt-operátor Hilbert–Schmidt-normáját úgy definiálják, mint:

${\displaystyle \|T\|_{2}=\left(\sum _{i\in I}\|Te_{i}\|_{W}^{2}\right)^{1/2}}$,

ahol ${\displaystyle (e_{i})_{i\in I}}$ ortonormált bázis ${\displaystyle V}$-ben. A Hilbert–Schmidt-norma a Frobenius-norma általánosítása végtelen dimenziós Hilbert-terekre. A Hilbert–Schmidt-normát indukálja az ${\displaystyle \langle T,S\rangle =\operatorname {spur} (S^{*}\,T)}$ skalárszorzat, ahol ${\displaystyle S^{*}}$ az ${\displaystyle S}$-hez adjungált operátor. A Hilbert–Schmidt-operátorok a Hilbert–Schmidt-normával Hilbert-teret alkotnak, ami ${\displaystyle V=W}$ esetén Banach-algebra, sőt H*-algebra.^[19]

Egy két szeparábilis Hilbert-tér közötti kompakt lineáris operátor árnyék-${\displaystyle p}$-normája, ahol ${\displaystyle 1\leq p<\infty }$:

${\displaystyle \|T\|_{p}=\left(\sum _{i=1}^{\infty }|s_{i}|^{p}\right)^{1/p}}$,

ahol ${\displaystyle (s_{i})}$ az operátor szinguláris értékeinek sorozata. Ha ${\displaystyle p=1}$, akkor a nyomnormához jutunk; ha ${\displaystyle p=2}$, akkor a Hilbert–Schmidt-normához. Az ${\displaystyle \ell ^{p}}$-beli szinguláris értékekkel bíró kompakt lineáris operátorok a megfelelő árnyék-${\displaystyle p}$-normával teljes normált teret alkotnak, ami ${\displaystyle V=W}$ esetén Banach-algebra.^[20]

Képek az egységgömbökről két dimenzióban:

• Egységgömbök két dimenzióban
• 
  p = 1
• 
  p = 2
• 
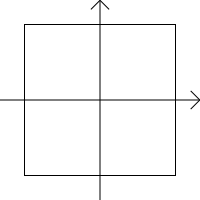  p = ∞

Egy adott ${\displaystyle x_{0}\in V}$ vektor és egy adott ${\displaystyle r\in {\mathbb {K} }}$ skalár esetén, ahol ${\displaystyle r>0}$, az

${\displaystyle \{x\in V\colon \|x-x_{0}\|<r\}}$    illetve    ${\displaystyle \{x\in V\colon \|x-x_{0}\|\leq r\}}$

halmazok nyílt, illetve zárt normagolyók. Az

${\displaystyle \{x\in V\colon \|x-x_{0}\|=r\}}$

halmaz az ${\displaystyle x_{0}}$ körüli ${\displaystyle r}$ sugarú normagömb. Ezek az elnevezések általánosítások: a normagömbnek és normagolyónak lehetnek csúcsai és élei, és csak az euklideszi vektornorma esetén egyezik meg az ismert gömbfogalommal. Ha ${\displaystyle x_{0}=0}$ és ${\displaystyle r=1}$, akkor egységgömbről és egységgolyóról beszélünk. Minden normagömb, illetve normagolyó megkapható az egységgömb, illetve az egységgolyó ${\displaystyle r}$-rel való skálázásával és az ${\displaystyle x_{0}}$ vektorral való eltolásával. Az egységgömb vektorai az egységvektorok; minden ${\displaystyle x\neq 0}$ vektor megkapható valamelyik egységvektor felszorzásával. Ez az egységvektor megkapható normálással: ${\displaystyle {\tfrac {x}{\|x\|}}}$.

A háromszög-egyenlőtlenség biztosítja, hogy a normagömb konvex legyen. Az abszolút homogenitás miatt középpontosan szimmetrikus az ${\displaystyle x_{0}}$ pontra. Véges dimenziós vektorterekben a normák normagömbbel is definiálhatók, amennyiben végesek, zártak, konvexek, tartalmazzák az origót és középpontosan szimmetrikusak rá. A megfelelő leképezés a Minkowski-funkcionál. Hermann Minkowski 1896-ban vizsgált ilyen funkcionálokat számelméleti kérdésekben.^[4]

A súlyozott normák súlyozott vektorterek normái. Például indukált súlyozott függvénynormát kapunk a ${\displaystyle w}$ súlyfüggvénnyel, úgy, hogy

${\displaystyle \|f\|_{w}={\sqrt {\langle f,f\rangle _{w}}}}$    ahol    ${\displaystyle \langle f,g\rangle _{w}=\int _{\Omega }w(x)f(x)g(x)\,dx}$,

ahol ${\displaystyle \langle \cdot ,\cdot \rangle _{w}}$ súlyozott ${\displaystyle L^{2}}$-skalárszorzat. A súlyfüggvények bevezetése lehetővé teszi függvényterek bővítését, mivel vannak függvények, melyek normája így már véges; vagy éppen szűkíti, például azokra a függvényekre, melyek monotonitása adott.

Ha gyengítjük a háromszög-egyenlőtlenséget úgy, hogy létezik egy ${\displaystyle k>1}$ konstans úgy, hogy ${\displaystyle x,y\in V}$

${\displaystyle \|x+y\|\leq k\cdot \left(\|x\|+\|y\|\right)}$

akkor kvázinormához jutunk. Egy kvázinormával ellátott vektortér kvázinormált tér. Például az ${\displaystyle \ell ^{p}}$-normák kvázinormák ${\displaystyle 0<p<1}$ esetén, és a hozzájuk tartozó terek kvázinormált terek, akár kvázi-Banach-terek.

A norma fogalma általánosítható úgy is, hogy valós vagy komplex vektortér helyett tetszőleges értékelt test fölötti vektorteret tekintünk, tehát olyan test fölötti vektorteret, ahol be van vezetve egy ${\displaystyle |\cdot |}$ abszolútérték.^[21] Ennek egy további általánosítás egy abszolútértékkel ellátott unitér gyűrű fölötti modulus. Legyen ${\displaystyle M}$ modulus egy abszolútértékkel ellátott ${\displaystyle (R,|\cdot |)}$ unitér gyűrű fölött! Ekkor egy ${\displaystyle \|\cdot \|\colon M\to \mathbb {R} _{+}}$ függvény norma ${\displaystyle M}$-ben, ha minden ${\displaystyle x,y\in M}$ vektorra és minden ${\displaystyle \alpha \in R}$ skalárra teljesülnek a norma tulajdonságai. Ha az ${\displaystyle R}$ gyűrűben az abszolútértéket pszeudoabszolútérték helyettesíti, és a homogenitást szubhomogenitásra gyengítjük, akkor pszeudonormát kapunk.

Ha egy ${\displaystyle V}$ vektorteret normával látunk el, akkor normált teret kapunk. A normált tereknek egyéb tulajdonságaik is vannak, így például távolságot is lehet bennük mérni, mivel a norma a vektorok közötti különbségképzéssel metrikát indukál:

Ha ${\displaystyle x,y\in V}$, akkor ${\displaystyle d(x,y)=\|x-y\|}$.

Ezzel a Fréchet-metrikával a normált tér metrikus tér is, és mivel a metrika topológiát indukál, topologikus tér, sőt, Hausdorff-tér is. A norma folytonos az általa indukált topológia szerint. Egy ${\displaystyle (x_{n})_{n}}$ pontosan akkor tart egy ${\displaystyle x}$ határértékhez, ha teljesül ${\displaystyle \|x_{n}-x\|\rightarrow 0}$. Ha minden Cauchy-sorozat határértékhez tart ebben a térben, akkor a tér teljes normált tér vagy Banach-tér.^[5]

Ha egy ${\displaystyle V}$ vektorteret ellátunk egy asszociatív és disztributív ${\displaystyle \circ }$ vektoriális szorzattal látunk el, akkor ${\displaystyle (V,+,\circ )}$ asszociatív algebra. Ha ${\displaystyle (V,\|\cdot \|)}$ normált tér, és normája szubmultiplikatív, és minden ${\displaystyle x,y\in V}$ vektorra

${\displaystyle \|x\circ y\|\leq \|x\|\cdot \|y\|}$,

akkor normált algebrához jutunk. Ha a normált tér teljes, akkor Banach-algebra.^[5] Például az ${\displaystyle {\mathbb {K} }^{n\times n}}$ négyzetes mátrixok tere a mátrixok összeadásával, a mátrixszorzással és egy szubmultiplikatív normával Banach-algebra.

Ha gyengítjük a definitséget, akkor félnormához jutunk. A homogenitás és a szubmultiplikativitás miatt az

${\displaystyle Z=\{x\in V\colon \|x\|=0\}}$

vektorok halmaza altér ${\displaystyle V}$-ben. Ezen a módon képezhető egy

${\displaystyle x\sim y:\Longleftrightarrow x-y\in Z}$

ekvivalenciareláció. Ha képezünk egy ${\displaystyle {\tilde {V}}}$ teret ennek a relációnak az ekvivalenciaosztályaival, akkor ${\displaystyle {\tilde {V}}}$ a ${\displaystyle \|\cdot \|}$ normával normált tér. Ezt a folyamatot a félnormára való maradékosztály-képzésnek nevezzük, és ${\displaystyle {\tilde {V}}}$ a ${\displaystyle V/Z}$ faktortérnek.^[22] Félnormák egy halmazával definiálhatók lokálisan konvex terek, amelyek speciális topologikus terek.

Két norma, ${\displaystyle \|\cdot \|_{a}}$ és ${\displaystyle \|\cdot \|_{b}}$ ekvivalens, ha vannak ${\displaystyle c_{1}}$ és ${\displaystyle c_{2}}$ konstansok úgy, hogy minden ${\displaystyle x\in V}$ esetén:

${\displaystyle c_{1}\|x\|_{b}\leq \|x\|_{a}\leq c_{2}\|x\|_{b}}$

azaz az egyik normával a másik alulról és felülről becsülhetők. Az ekvivalens normák ugyanazt a topológiát indukálják. Ha egy sorozat konvergál az egyik normában, akkor az ekvivalens normában is konvergál.^[23]

Véges dimenziós terekben minden norma ekvivalens, ugyanis a normagömbök a Heine–Borel-tétel miatt kompakt halmazok. Végtelen dimenziós terekben vannak nem ekvivalens normák. Ha egy vektortér teljes két normában, akkor ezek ekvivalensek akkor, ha van egy pozitív ${\displaystyle c}$ konstans úgy, hogy:

${\displaystyle \|x\|_{a}\leq c\|x\|_{b}}$

merthogy van egy két Banach-tér közötti folytonos leképezés, melynek inverze a nyílt leképezés tétele szerint szintén folytonos.

Egy ${\displaystyle \mathbb {K} }$ test fölötti ${\displaystyle V}$ normált vektortér ${\displaystyle V^{*}}$ duális tere a ${\displaystyle V}$-ből ${\displaystyle \mathbb {K} }$-ba menő folytonos lineáris funkcionálok tere. Például az ${\displaystyle n}$-dimenziós vektorok terének duális tere a vektorkomponensek lineáris kombinációja, ami egy ugyanolyan dimenziós vektortér. Egy ${\displaystyle \|\cdot \|}$ normához duális ${\displaystyle \|\cdot \|^{\ast }}$ funkcionálnorma:

${\displaystyle \|L\|^{\ast }=\sup _{\|x\|\leq 1}|L\,x|=\sup _{\|x\|\not =0}{\frac {|L\,x|}{\|x\|}}}$.

Ezzel a normával a duális tér szintén normált tér, sőt teljes normált tér, függetlenül attól, hogy a kiindulási tér teljes-e.^[24] Ha két norma ekvivalens, akkor duális normáik is ekvivalensek. A duális normákra a szuprémumértelmezésével következik, hogy:

${\displaystyle |L\,x|\leq \|L\|^{\ast }\|x\|}$.

• Stoyan Gisbert - Takó Galina: Numerikus módszerek 1.
• Riesz-Szőkefalvi: Funkcionálanalízis
• Hans Wilhelm Alt. Lineare Funktionalanalysis, 6., überarb. Aufl., Berlin Heidelberg: Springer (2012. július 21.) 
• Albrecht Beutelspacher. Lineare Algebra: eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen, 8., aktualis. Aufl, Wiesbaden: Springer Spektrum (2014. július 21.) 
• Elena Deza, Michel Marie Deza. Encyclopedia of Distances (angol nyelven). Springer Berlin Heidelberg (2009. július 21.) 
• Gerd Fischer, Boris Springborn. Lineare Algebra. Eine Einführung für Studienanfänger, 19., vollständig überarbeitete und ergänzte Auflage, Berlin [Heidelberg]: Springer Spektrum (2020. július 21.) 
• Hans Rudolf Schwarz, Norbert Köckler. Numerische Mathematik. Wiesbaden: Vieweg+Teubner Verlag (2011. július 21.) 
• Dirk Werner. Funktionalanalysis, 8., vollständig überarbeitete Auflage, Berlin: Springer Spektrum (2018. július 21.) 

Ez a szócikk részben vagy egészben a Norm (Mathematik) című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.