流線曲率の定理 (りゅうせんきょくりつのていり、英語 : Streamline Curvature Theorem )は、非粘性流体 (完全流体 ) の外力が無視できる定常な流れにおいて、流線 の曲率中心 方向に圧力 が低くなることを述べた定理である[1] [2] ベルヌーイの定理 と同様に、流線曲率の定理は定常オイラー方程式の成分分解から得られる。
流線曲率の定理は次のように説明される。
流跡線(定常前提であり流線と同じ)の曲がるところでは方向の変化に対し相応の加速度 (向心加速度) が生じている。粘性/外力のなしの状況では圧力勾配以外に加速度はない。したがって曲線の外側から内側へむけて圧力が低い分布となっている。
r {\displaystyle r}
外力がない、定常 ・非粘性 な流れにおいて ∂ p ∂ r = ρ v 2 r ( > 0 ) {\displaystyle {\partial p \over \partial r}=\rho {v^{2} \over r}~(>0)} が成り立つ。ただし、 p {\displaystyle p} 圧力 、 ρ {\displaystyle \rho } 密度 、 v {\displaystyle v} 速さ である。 流線曲率の定理は
流れと一緒に動く系からみたとき、単位体積あたりの遠心力 と動径方向の圧力勾配が釣り合う
と解釈してもよい。渦 の中心が周囲より低圧であることは流線曲率の定理を使って理解できる。
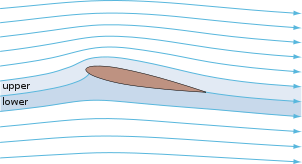
流線曲率の定理により、翼上面の気圧は無限遠方 (上) の気圧より低く、翼下面の気圧は無限遠方 (下) の気圧より高い。無限遠方での気圧は上下ともに大気圧だから、翼の上面の圧力は下面の圧力より低い。この圧力差が揚力 を発生させる。 翼が揚力 を発生するメカニズムの説明にベルヌーイの定理が使われることが多いが、流線曲率の定理でも説明することが可能である。(図を参照)
なお、英語名の"Streamline Curvature Theorem"は日本でしか通じない。英語圏の文献ではこの概念を表す一般的な名称はない[3]
外力なし、定常かつ非粘性の運動方程式(定常オイラー方程式)
v ⋅ ∇ v = − 1 ρ ∇ p {\displaystyle {\boldsymbol {v}}\cdot \nabla {\boldsymbol {v}}=-{1 \over \rho }\nabla p} を考える。ここで v {\displaystyle {\boldsymbol {v}}} p {\displaystyle p} ρ {\displaystyle \rho } 速度 、圧力 、密度 を表す。
この方程式を、 流線に対する 接単位ベクトル e s {\displaystyle {\boldsymbol {e}}_{s}} e n {\displaystyle {\boldsymbol {e}}_{n}} e b {\displaystyle {\boldsymbol {e}}_{b}} フレネ・セレ標構 { e s , e n , e b } {\displaystyle \{{\boldsymbol {e}}_{s},{\boldsymbol {e}}_{n},{\boldsymbol {e}}_{b}\}} [4]
流線は流れの速度ベクトルに接する曲線であるから、運動方程式の左辺は、以下のように記述できる:
v ⋅ ∇ v = v ∂ ∂ s ( v e s ) ( v = v e s , ∂ / ∂ s ≡ e s ⋅ ∇ ) = v ∂ v ∂ s e s + v 2 R e n ( ∵ ∂ e s ∂ s = 1 R e n ) {\displaystyle {\begin{aligned}{\boldsymbol {v}}\cdot \nabla {\boldsymbol {v}}&=v{\partial \over \partial s}(v{\boldsymbol {e}}_{s})&({\boldsymbol {v}}=v{\boldsymbol {e}}_{s},~{\partial /\partial s}\equiv {\boldsymbol {e}}_{s}\cdot \nabla )\\&=v{\partial v \over \partial s}{\boldsymbol {e}}_{s}+{v^{2} \over R}{\boldsymbol {e}}_{n}&(\because ~{\partial {\boldsymbol {e}}_{s} \over \partial s}={1 \over R}{\boldsymbol {e}}_{n})\end{aligned}}} ここで R {\displaystyle R} 曲率半径 である。
よって、定常非粘性流れの運動方程式は以下のようになる。
{ v ∂ v ∂ s = − 1 ρ ∂ p ∂ s v 2 R = − 1 ρ ∂ p ∂ n ( ∂ / ∂ n ≡ e n ⋅ ∇ ) 0 = − 1 ρ ∂ p ∂ b ( ∂ / ∂ b ≡ e b ⋅ ∇ ) {\displaystyle {\begin{cases}\displaystyle v{\partial v \over \partial s}=-{1 \over \rho }{\partial p \over \partial s}\\\displaystyle {v^{2} \over R}=-{1 \over \rho }{\partial p \over \partial n}&({\partial /\partial n}\equiv {\boldsymbol {e}}_{n}\cdot \nabla )\\\displaystyle 0=-{1 \over \rho }{\partial p \over \partial b}&({\partial /\partial b}\equiv {\boldsymbol {e}}_{b}\cdot \nabla )\end{cases}}} 第2式において、r を曲率中心からの距離として方程式を書き換える。e n = - e r であることから ∂ p ∂ n {\displaystyle {\partial p \over \partial n}} − ∂ p ∂ r {\displaystyle -{\partial p \over \partial r}} R をr に書き換えれば、 流線曲率定理
∂ p ∂ r = ρ v 2 r {\displaystyle {\partial p \over \partial r}=\rho {v^{2} \over r}} が得られる。
バロトロピック 流れ ( ρ = ρ ( p ) {\displaystyle \rho =\rho (p)}
∂ ∂ s ( v 2 2 + ∫ d p ρ ) = 0 {\displaystyle {\partial \over \partial s}\left({v^{2} \over 2}+\int {\mathrm {d} p \over \rho }\right)=0} と変形でき、ベルヌーイの定理 を導ける。第3式は従法線方向に圧力は一定であることを表している。
^ 今井 功『流体力学(前編)』裳華房、1973年11月。ISBN 4785323140。 ^ 高木 正平. “なぜ翼に揚力が発生するか?:ベルヌーイの定理か流線曲率の定理か(特集 科学と工学における論争) How do Wings Generate Lift : Bernoulli Theorem or Streamline-Curvature Theorem”. 2012年10月9日 閲覧。 ^ Babinsky, Holger (November 2003), “How do wings work?”, Physics Education 38 (6): 497–503, Bibcode: 2003PhyEd..38..497B, doi:10.1088/0031-9120/38/6/001, http://www.iop.org/EJ/article/0031-9120/38/6/001/pe3_6_001.pdf ^ James A. Fay (June 1994). Introduction to Fluid Mechanics . MIT Press. ISBN 0262061651
石綿良三・根本光正著 日本機械学会編 「流れのふしぎ 遊んでわかる流体力学のABC」 2004年08月20日発行 ISBN 978-4-06-257452-5