階段関数

階段関数（かいだんかんすう、英: step functionまたは英: staircase function）とは、おおまかに言って、グラフが階段状になる実関数のことである。より正確には、区間上の指示関数が有限^[要出典]個あって、それらの線型結合で表される関数である。有限個^[要出典]のみの区分を持った、区分的に定数関数である関数とも表現できる。

関数 f : R → R が階段関数であるとは、ある正整数 n が存在して、n 個の実数 α₁,..., α_n と n 個の区間 A₁,..., A_n 上の指示関数 χ₁,..., χ_n によって、

${\displaystyle f(x)=\sum _{i=1}^{n}\alpha _{i}\chi _{i}(x)}$

と表されることをいう。ここに、集合 A 上の指示関数 χ_A とは、次で定義されるものであった。

${\displaystyle \chi _{A}(x)={\begin{cases}1,&\ (x\in A),\\0,&\ (x\notin A).\end{cases}}}$

この定義において、区間 A_i たちは、次の2条件を満たすとしてもよい。

• 互いに素である。すなわち、i ≠ j のとき、A_i ∩ A_j = ∅ である。
• 和集合が実数全体である。すなわち、A₁ ∪ … ∪ A_n = R である。

例えば、この条件を満たさずに階段関数

${\displaystyle f=4\chi _{[-5,1)}+3\chi _{(0,6)}}$

が与えられたならば、条件を満たすように

${\displaystyle f=0\chi _{(-\infty ,-5)}+4\chi _{[-5,0]}+7\chi _{(0,1)}+3\chi _{[1,6)}+0\chi _{[6,\infty )}}$

と表現することもできる。

• 定数関数は自明な階段関数である。階段関数の定義において、n = 1, A₁ = R として得られる。
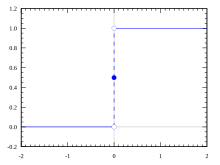
• ヘヴィサイドの階段関数は、しばしば応用に用いられる重要な階段関数である。n = 3, A₁ = (-∞ 0), A₂ = [0, 0], A₃ = (0, ∞) として得られる。

• 矩形関数は、R を5つの区間に分けて得られる階段関数である。

• 床関数や天井関数は、無限個の区間に分けて与えられるため、ここでの文脈においては階段関数ではない。

階段関数のとる値は、有限個の可能性しかない。階段関数の定義において、区間 A_i たちを互いに素な R の分割にとっておけば、A_i の任意の元 x に対して f(x) = α_i となる。

階段関数

${\displaystyle f(x)=\sum _{i=1}^{n}\alpha _{i}\chi _{A_{i}}(x)}$

のルベーグ積分は、区間 A_i の長さ L (A_i) が全て有限である場合、

${\displaystyle \int _{\mathbb {R} }fdx=\sum _{i=1}^{n}\alpha _{i}L(A_{i})}$

で与えられる。

2つの階段関数の和や積もまた階段関数である。この演算により、階段関数全体の集合は R 上の代数を成す。

• 単関数
• カントール関数