Besselfunctie

Besselfuncties zijn oplossingen van de besselse differentiaalvergelijking. Ze worden zo genoemd naar de wiskundige en astronoom Friedrich Wilhelm Bessel, die de vergelijking uitwerkte. Hij deed dit met het doel de verstoring te berekenen die drie hemellichamen op elkaars baan uitoefenen; voorbereidend werk was door anderen gedaan, maar Bessels vergelijking was meer algemeen geldig. Besselfuncties worden onderscheiden naar besselfuncties van de eerste soort en van de tweede soort. De besselfunctie van de eerste soort van de orde ${\displaystyle a}$ wordt genoteerd als ${\displaystyle J_{a}}$, en die van de tweede soort van de orde ${\displaystyle a}$ als ${\displaystyle Y_{a}}$.

De besselvergelijking kan echter ook worden gebruikt om oplossingen te vinden voor de vergelijkingen van Laplace en van Helmholtz, wanneer daarbij cilindercoördinaten worden gebruikt. Daardoor zijn besselfuncties vooral van belang bij veel vraagstukken uit de wiskundige natuurkunde, zoals vragen omtrent golfvoortplanting, statische spanning enzovoort. Enkele voorbeelden zijn:

• elektromagnetische golven in een cilindrische golfgeleider
• warmtegeleiding in een cilindervormig voorwerp
• trillingswijzen van een dun cirkel- of ringvormig membraan
• verstrooiingsproblemen in een tralie.
• componentamplitudes bij frequentiemodulatie (FM): zie de grafiek Media:Bessels.png
• bepaling van grondwaterstanden bij onttrekkingen.

Besselfuncties zijn oplossingen ${\displaystyle y(x)}$ van de besselse differentiaalvergelijking:

${\displaystyle x^{2}y''(x)+xy'(x)+(x^{2}-n^{2})y(x)=0}$

Oplossingen zijn ${\displaystyle y(x)=J_{a}(x)}$ en ${\displaystyle y(x)=Y_{a}(x)}$.

Voor ${\displaystyle a\notin \mathbb {Z} }$ zijn ${\displaystyle J_{a}}$ en ${\displaystyle J_{-a}}$ lineair onafhankelijk, zodat voor de algemene oplossing geldt:

${\displaystyle y(x)=c_{1}J_{a}(x)+c_{2}J_{-a}(x)}$

in het bijzonder is

${\displaystyle Y_{a}(x)={\frac {J_{a}(x)\cos(a\pi )-J_{-a}(x)}{\sin(a\pi )}}}$

Voor ${\displaystyle a=n\in \mathbb {Z} }$ is

${\displaystyle J_{-n}(x)=(-1)^{n}J_{n}(x)}$,

dus zijn ${\displaystyle J_{n}}$ en ${\displaystyle J_{-n}}$ lineair afhankelijk.

Ook is

${\displaystyle Y_{-n}(x)=(-1)^{n}Y_{n}(x)}$

waarin

${\displaystyle Y_{n}(x)=\lim _{a\to n}Y_{a}(x)}$

dus zijn ook ${\displaystyle Y_{n}}$ en ${\displaystyle Y_{-n}}$ lineair afhankelijk. Wel zijn ${\displaystyle J_{n}}$ en ${\displaystyle Y_{n}}$ lineair onafhankelijk, zodat in dit geval de algemene oplossing geschreven kan worden als

${\displaystyle y(x)=c_{1}J_{n}(x)+c_{2}Y_{n}(x)}$

De besselfuncties van de eerste soort worden gegeven door de complexe integraal:

${\displaystyle J_{n}(x)={\frac {1}{2{\pi }i}}\oint _{\!\!\!C}{\frac {g(x,z)}{z^{n+1}}}\,\mathrm {d} z}$

met ${\displaystyle C}$ een geschikte contour en ${\displaystyle g(x,z)}$ de voortbrengende functie gegeven door:

${\displaystyle g(x,z)=e^{{\frac {x}{2}}(z-{\frac {1}{z}})}=\sum _{n=-\infty }^{\infty }J_{n}(x)z^{n}}$

De besselfuncties van de eerste soort hebben de machtreeksontwikkeling

${\displaystyle J_{a}(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!\,\Gamma (k+a+1)}}{\left({\frac {x}{2}}\right)}^{2k+a}}$,

die met de methode van Frobenius afgeleid kan worden^[1]

De besselfuncties voldoen aan de recursieve betrekkingen:

${\displaystyle J_{n-1}(x)+J_{n+1}(x)={\frac {2n}{x}}J_{n}(x)}$

${\displaystyle J_{n-1}(x)-J_{n+1}(x)=2J_{n}'(x)}$

Een berekening leert dat de besselfunctie van de eerste soort en van de nulde orde gegeven wordt door:

${\displaystyle J_{0}(x)={\frac {2}{\pi }}\int _{0}^{1}{\frac {\cos(xt)}{\sqrt {1-t^{2}}}}\,\mathrm {d} t}$

Als we ${\displaystyle J_{0}(x)}$ plotten dan verkrijgen we het volgende resultaat:

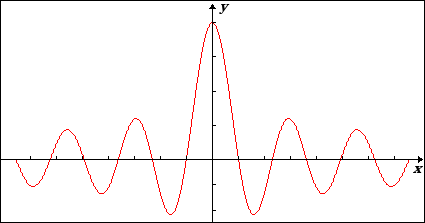
${\displaystyle J_{0}(x)}$ bereikt haar maximale amplitude in de oorsprong. Naarmate ${\displaystyle x}$ zich verwijdert van de oorsprong neemt de amplitude geleidelijk af om dan uiteindelijk te verdwijnen in het oneindige (${\displaystyle x\to +\infty }$, ${\displaystyle x\to -\infty }$).

Zie de categorie Bessel functions van Wikimedia Commons voor mediabestanden over dit onderwerp.