Brachistochrona

Ten artykuł od 2018-03 wymaga zweryfikowania podanych informacji. Należy podać wiarygodne źródła w formie przypisów bibliograficznych. Część lub nawet wszystkie informacje w artykule mogą być nieprawdziwe. Jako pozbawione źródeł mogą zostać zakwestionowane i usunięte. Sprawdź w źródłach: Encyklopedia PWN • Google Books • Google Scholar • Federacja Bibliotek Cyfrowych • BazHum • BazTech • RCIN • Internet Archive (texts / inlibrary) Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

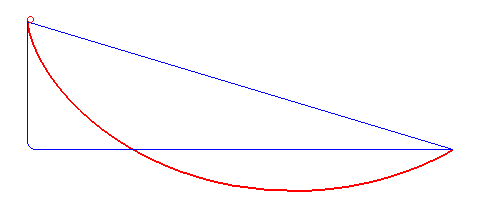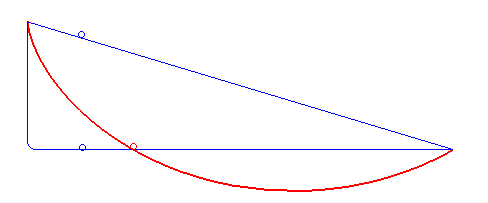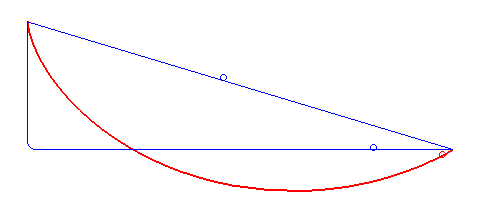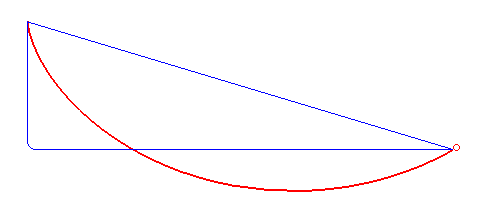
Brachistochrona, krzywa najkrótszego spadku (gr. βραχιστoς brachistos – „najkrótszy” + χρovoς chronos – „czas”) – krzywa, po której masa punktowa pod wpływem stałej siły (siły ciężkości) stacza się w możliwie najkrótszym czasie. Brachistochrona jest fragmentem cykloidy^[1].

Zagadnienie brachistochrony było jednym z pierwszych, do rozwiązania którego wykorzystano rachunek wariacyjny. Problem brachistochrony postawiony został w 1696 przez Johanna Bernoulliego, był wynikiem rywalizacji braci Jakoba oraz Johanna Bernoullich^[2]. Problem znalezienia krzywej najszybszego spadku został rozwiązany niezależnie przez Leibniza, Newtona, Johanna Bernoulliego oraz de l’Hospitala.

Przy założeniu, że równaniem szukanej krzywej jest ${\displaystyle y=y(x),}$ punkty ${\displaystyle A}$ i ${\displaystyle B}$ można zapisać następująco:

${\displaystyle A=(a,y(a))}$ oraz ${\displaystyle B=(b,y(b)).}$

Rodzina funkcji (funkcjonał) spełniających założenia problemu jest opisana jako:

${\displaystyle F(y(x))=\int \limits _{a}^{b}{\frac {ds}{v}},}$

gdzie:

${\displaystyle ds={\sqrt {1+y'(x)^{2}}}dx}$ – długość krzywej,

${\displaystyle v=y'(x)}$ – prędkość, którą można wyznaczyć z zasady zachowania energii:

${\displaystyle {\frac {1}{2}}mv^{2}=mg(y(a)-y(x)),}$

stąd:

${\displaystyle v={\sqrt {2g(y(a)-y(x))}}.}$

Wyrażenia na ${\displaystyle ds}$ i ${\displaystyle v}$ można teraz wstawić do wyjściowej całki:

${\displaystyle F(y(x))=\int \limits _{a}^{b}{\sqrt {\frac {1+y'(x)^{2}}{2g(y(a)-y(x))}}}dx.}$

Nie zmniejszając ogólności rozważań można przyjąć punkt ${\displaystyle A}$ jako ${\displaystyle A=(0,0),}$ co upraszcza dalsze rachunki. Dodatkowo można założyć również, że oś ${\displaystyle y}$ skierowana jest do dołu. Zatem aby rozwiązać postawione zagadnienie, należy wyznaczyć ekstremum (minimum) funkcjonału:

${\displaystyle F(y(x))=\int \limits _{0}^{b}{\sqrt {\frac {1+y'(x)^{2}}{2gy(x)}}}dx.}$

Jako że zadana całka nie zależy jawnie od zmiennej ${\displaystyle x}$ można zamiast równania Eulera zastosować tożsamość Beltramiego ${\displaystyle (f-y'{\frac {\partial f}{\partial y'}}=C){:}}$

${\displaystyle {\sqrt {\frac {1+y'(x)^{2}}{2gy(x)}}}-{\sqrt {\frac {2gy(x)}{1+y'(x)^{2}}}}{\frac {y'(x)^{2}}{2gy(x)}}=C,}$

gdzie ${\displaystyle C}$ oznacza pewną stałą. Po uproszczeniu powyższego wyrażenia otrzymuje się:

${\displaystyle y(x)(1+y'(x)^{2})={\frac {1}{2gC^{2}}}=k^{2}.}$

Jest to równanie różniczkowe, którego rozwiązaniem jest cykloida postaci:

${\displaystyle x(\theta )={\frac {1}{2}}k^{2}(\theta -\sin \theta ),}$

${\displaystyle y(\theta )={\frac {1}{2}}k^{2}(1-\cos \theta ).}$

• rachunek wariacyjny
• tautochrona

• Grant Sanderson, The Brachistochrone, with Steven Strogatz, kanał 3blue1brown, YouTube, 1 sierpnia 2016 [dostęp 2021-03-15].
• Michael Stevens, The Brachistochrone, kanał Vsauce na YouTube, 21 stycznia 2017 [dostęp 2021-03-15].