Epimorfizm

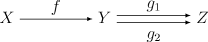
Epimorfizm – w teorii kategorii, morfizm ${\displaystyle f\colon X\to Y}$ mający prawostronną własność skracania, tj. dla wszystkich morfizmów ${\displaystyle g_{1},g_{2}\colon Y\to Z}$ spełniony jest warunek^[1]:

${\displaystyle g_{1}\circ f=g_{2}\circ f\Rightarrow g_{1}=g_{2}.}$

Epimorfizmy są odpowiednikami funkcji „na”, lecz nie są one z nimi tożsame. Pojęciem dualnym do epimorfizmu jest monomorfizm.

Wielu autorów książek o algebrze abstrakcyjnej i uniwersalnej definiuje epimorfizm jako homomorfizm „na” (surjektywny)^[2]. Każdy epimorfizm w tym sensie algebraicznym jest epimorfizmem w sensie teorii kategorii, ale nie jest to prawdą we wszystkich kategoriach.

Epimorfizm konormalny

Jeśli dany epimorfizm jest kojądrem jakiegoś morfizmu, to nazywany jest on wówczas epimorfizmem konormalnym^[3].

Jeśli każdy epimorfizm danej kategorii jest epimorfizmem konormalnym, to nazywa się kategorią konormalną. Każda z kategorii Gr, Ab, Vect jest konormalna. Kojądro w tych kategoriach istnieje dla każdego morfizmu

${\displaystyle \alpha \colon A\to B.}$

Jest ono równe grupie ilorazowej ${\displaystyle B/G,}$ gdzie ${\displaystyle G}$ jest najmniejszą podgrupą normalną zawierającą ${\displaystyle \alpha (A).}$

Przykłady

• Epimorfizmami w kategorii Set są odwzorowania „na”.

Niech ${\displaystyle f\colon X\to Y}$ będzie epimorfizmem, a jednocześnie istnieje taki ${\displaystyle y_{0}\in Y\setminus f(X).}$ Niech ${\displaystyle y_{1}\in f(X).}$ Niech ${\displaystyle Z=\{y_{0},y_{1}\}}$ oraz

${\displaystyle g_{0}(y)=y_{0}}$ dla ${\displaystyle y\in Y,}$

${\displaystyle g_{1}(y)={\begin{cases}y_{0},&y\in f(X)\\y_{1},&y\notin f(X)\end{cases}}.}$

Wtedy ${\displaystyle g_{0}f=g_{1}f}$ i ${\displaystyle g_{0}\neq g_{1},}$ co jest sprzeczne z tym, że ${\displaystyle f}$ jest epimorfizmem. Zatem nie istnieje ${\displaystyle y_{0}\in Y\setminus f(X)}$ i funkcja ${\displaystyle f}$ jest „na”.

• Morfizmy identycznościowe są epimorfizmami.

Zobacz też

• izomorfizm
• monomorfizm

Przypisy

Bibliografia

• Zbigniew Semadeni, Antoni Wiweger: Wstęp do teorii kategorii i funktorów. Wyd. 2. Warszawa: Państwowe Wydawnictwo Naukowe, 1978, seria: Biblioteka Matematyczna. Tom 45.

Literatura dodatkowa

• Bucur I., Deleanu A.: Introduction to the Theory of Categories and Functors (tłum. ros.). Москва: Мир, 1972. Brak numerów stron w książce
• Jiri Adámek, Horst Herrlich, George E. Strecker: Abstract and Concrete Categories. 2005-01-18. [dostęp 2011-08-26]. (ang.).