Twierdzenie Seiferta-van Kampena

Twierdzenie Seiferta-van Kampena w topologii algebraicznej pozwala wyrazić grupę podstawową sumy spójnej zbiorów otwartych w zależności od grup podstawowych poszczególnych składników.

Treść twierdzenia

Niech ${\displaystyle X}$ będzie łukowo spójną przestrzenią topologiczną będącą sumą zbiorów otwartych ${\displaystyle U_{1}}$ oraz ${\displaystyle U_{2}}$ takich, że ${\displaystyle x_{0}\in U_{1}\cap U_{2},}$ gdzie ${\displaystyle x_{0}}$ jest punktem bazowym wszystkich grup podstawowych wspomnianych w twierdzeniu. Niech ${\displaystyle j_{i}:U_{i}\hookrightarrow X}$ będą włożeniami. Wtedy grupa podstawowa sumy ${\displaystyle U_{1}\cup U_{2}}$ jest produktem wolnym grup podstawowych ${\displaystyle \pi _{1}(U_{1},x_{o})}$ oraz ${\displaystyle \pi _{1}(U_{2},x_{o})}$ z amalgamacją wzdłuż ${\displaystyle \pi _{1}(U_{1}\cap U_{2},x_{o})}$ oraz przemienny jest diagram

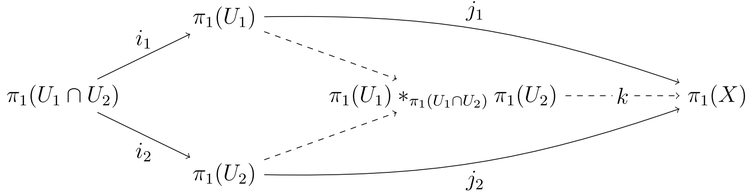gdzie odwzorowania ${\displaystyle i_{\alpha },j_{\alpha }}$ są dla ${\displaystyle \alpha \in \{1,2\}}$ indukowane przez stosowne włożenia, zaś naturalny homomorfizm ${\displaystyle k}$ jest izomorfizmem.

Szczególne przypadki: ${\displaystyle \pi _{1}(U_{1})=0}$

Jeśli ${\displaystyle \pi _{1}(U_{1})=0}$ wtedy ${\displaystyle \pi _{1}(X)=\pi _{1}(U_{2})/\pi _{1}(U_{1}\cap U_{2}),}$ co oznacza że doklejenie ściągalnej przestrzeni topologicznej powoduje że wynikowa grupa podstawowa jest grupą ilorazową z klasami równoważności danymi przez ściągalne pętle w części wspólnej ${\displaystyle U_{1}}$ i ${\displaystyle U_{2}.}$

Szczególne przypadki: ${\displaystyle \pi _{1}(U_{1}\cap U_{2})=0}$

Jeśli ${\displaystyle \pi _{1}(U_{1}\cap U_{2})=0}$ (na przykład kiedy ${\displaystyle U_{1}\cap U_{2}}$ jest ściągalna) wtedy produkt wolny z amalgamacją upraszcza się do produktu wolnego grup podstawowych. Ten szczególny przypadek po odpowiednich przekształceniach prowadzi do twierdzenia van Kampena o bukietach.

Twierdzenie van Kampena o bukietach

Pokrewne twierdzenie, które nie jest szczególnym przypadkiem twierdzenia Seiferta-van Kampena (punkt nie jest zbiorem otwartym), zachodzi dla bukietów.

Niech ${\displaystyle X}$ będzie bukietem przestrzeni ${\displaystyle A}$ oraz ${\displaystyle B,}$ tj. ${\displaystyle X=A\vee B.}$ Wtedy zachodzi następujący izomorfizm grup podstawowych zaczepionych w punkcie bazowym bukietu:

${\displaystyle \pi _{1}(X)\cong \pi _{1}(A)*\pi _{1}(B).}$

Czyli grupa podstawowa bukietu jest produktem wolnym grup podstawowych składników bukietu.

Bibliografia

• Roman Duda: Wprowadzenie do topologii. Część II. Topologia algebraiczna i topologia rozmaitości. Warszawa: PWN, 1986. Brak numerów stron w książce
• Allen Hatcher: Algebraic topology. Cambridge: Cambridge University Press, 2002. ISBN 0-521-79160-X. Brak numerów stron w książce
• Peter May: A Concise Course in Algebraic Topology. University of Chicago Press, 1999. ISBN 0-226-51183-9. Brak numerów stron w książce