Podudarnost (geometrija)

U geometriji dve figure su podudarne ako imaju istu veličinu i oblik, ili ako jedna ima isti oblik i veličinu kao slika u ogledalu druge.^[3] Dva skupa tačaka su podudarna ako postoji preslikavanje kojim se taj skup preslikava u drugi skup, a da se pri tom ne menja veličina i oblik.

Podudarnost se označava sa ${\displaystyle \cong }$

Podudaran ima značenje:^[4]

1. Dve duži su podudarne ako imaju istu dužinu ${\displaystyle d_{1}=d_{2}}$ tj ${\displaystyle d_{1}\cong d_{2}}$
2. Dva ugla su podudarna ako imaju istu meru ${\displaystyle \alpha _{1}=\alpha _{2}}$ tj ${\displaystyle \alpha _{1}\cong \alpha _{2}}$
3. Dva kruga su podudarna ako imaju isti prečnik ${\displaystyle R_{1}\cong R_{2}}$ tj ${\displaystyle R_{1}\cong R_{2}}$

Da bi dva poligona bila podudarna, moraju imati jednak broj stranica (a samim tim i jednak broj – isti broj – temena). Dva poligona sa n strana su podudarna ako i samo ako svaki od njih ima numerički identične nizove (čak i ako u smeru kazaljke na satu za jedan poligon i suprotno od kazaljke na satu za drugi) stranica-ugao-stranica-ugao- ... za n stranica i n uglova.

Kongruencija poligona može se grafički utvrditi na sledeći način:

• Prvo, uparite i označite odgovarajuće vrhove dve figure.
• Drugo, nacrtajte vektor od jednog od vrhova jedne od figura do odgovarajućeg temena druge figure. Translirajte prvu figuru ovim vektorom tako da se ova dva temena poklapaju.
• Treće, rotirajte transliranu figuru oko podudarnog temena dok se jedan par odgovarajućih strana ne poklopi.
• Četvrto, odrazite rotiranu figuru oko ove uparene strane dok se brojke ne poklope.

Ako u bilo kom trenutku korak ne može da se završi, poligoni nisu podudarni.

Aksiomi podudarnosti opisuju osnovne karakteristike relacije podudarnosti parova tačaka. Ovu relacija se uvodi kao polazni pojam.

• Aksiom 1

Ako je ${\displaystyle (A,B)\cong (C,D)}$ i ${\displaystyle A=B}$, tada je i ${\displaystyle C=D}$.

• Aksiom 2

Za svake dve tačke ${\displaystyle A}$ i ${\displaystyle B}$ je ${\displaystyle (A,B)\cong (B,A)}$.

• Aksiom 3

Ako je ${\displaystyle (A,B)\cong (C,D)}$ i ${\displaystyle (A,B)\cong (E,F)}$ tada je ${\displaystyle (C,D)\cong (E,F)}$

• Aksiom 4

Ako su C i C' tačke otvorenih duži AB i A'B', takve da je ${\displaystyle (A,C)\cong (A',C')}$ i ${\displaystyle (B,C)\cong (B',C')}$, tada je i ${\displaystyle (B,C)\cong (A',B')}$

• Aksiom 5

Ako su A i B dve tačke i CX poluprava tada na toj polupravoj postoji tačka D takva da je ${\displaystyle (A,B)\cong (C,D)}$

• Aksiom 6

Ako su A, B, C tri nekolinearne tačke i ${\displaystyle A',B'}$ tačke ruba neke poluravni ${\displaystyle \pi }$, takve da je ${\displaystyle (A,B)\cong (A',B')}$ tada u toj poluravni postoji jedinstvena tačka C' takva da je ${\displaystyle (A,C)\cong (A',C')}$ i ${\displaystyle (B,C)\cong (B',C')}$

• Aksiom 7

Ako su A, B, C i A', B', C' dve trojke nekolinearnih tačaka i D i D' tačke polupravih BC i B'C' takve da je ${\displaystyle (AB)\cong (A',B')}$ , ${\displaystyle (BC)\cong (B',C')}$, ${\displaystyle (A,C)\cong (A',C')}$ i ${\displaystyle (B,D)\cong (B',D')}$, tada je i ${\displaystyle (A,D)\cong (A',D')}$

Relacija podudarnosti parova tačaka je relacija ekvivalencije.

1. ${\displaystyle (A,B)\cong (A,B)}$ relacija je refleksivna.
2. Neka je ${\displaystyle (AB)\cong (C,D)}$ [${\displaystyle (A,B)\cong (A,B)}$] => ${\displaystyle (CD)\cong (A,B)}$ relacija je simetrična
3. ${\displaystyle (A,B)\cong (C,D)}$ i ${\displaystyle (C,D)\cong (E,F)=>}$ ${\displaystyle (A,B)\cong (E,F)}$ [sledi na osnovu simetričnosti]

Teorema 1

Ako su A i B dve tačke i CX poluprava tada na toj polupravoj postoji jedinstvena tačka D takva da je '${\displaystyle (A,B)\cong (CD)}$

Teorema 2

Ako su A,B,C tri razne tačke prave p i A',B' dve tačke prave p' takve da je ${\displaystyle (A,B)\cong (A',B')}$, tada postoji jedinstvena tačka C' takva da je A',B' i ${\displaystyle (A,C)\cong (A',C')}$.

Pri tome, tačka C' pripada pravoj p' i:

1. ako je ${\displaystyle {\mathfrak {B}}(A,C,B)}$, tada je ${\displaystyle {\mathfrak {B}}(A',C',B')}$
2. ako je ${\displaystyle {\mathfrak {B}}(A,B,C)}$, tada je ${\displaystyle {\mathfrak {B}}(A',B',C')}$
3. ako je ${\displaystyle {\mathfrak {B}}(B,C,A)}$, tada je ${\displaystyle {\mathfrak {B}}(B',C',A')}$

Definicija 1

Kaže se da je uređena n-torka tačaka ${\displaystyle (A_{1},A_{2},...,A_{n})}$ podudarna sa n-torkom ${\displaystyle (A'_{1},A'_{2},...,A'_{n})}$ u oznaci ${\displaystyle (A_{1},A_{2},...,A_{n})\cong (A'_{1},A'_{2},...,A'_{n})}$

ako je za svako ${\displaystyle (i,k)\in {\begin{Bmatrix}{1,2,...n}\end{Bmatrix}}(A_{i},A_{k})\cong (A'_{i},A'_{k})}$

Definicija 2

Neka su A i B dve razne tačke neke ravni ${\displaystyle \alpha }$. Skup svih tačaka ${\displaystyle X}$ te ravni takvih da je ${\displaystyle (A,B)\cong (A,X)}$, naziva se krug, u oznaci ${\displaystyle k(A,AB)}$, sa centrom A i čiji je poluprečnik duž AB.

Ako su dve duži AB i CD su podudarne, to može se označiti sa ${\displaystyle AB\cong CD}$

Teorema 3

${\displaystyle (A,B)\cong (A',B')=>A,B\cong A',B'}$,

Definicija 3

Tačka S je središte duži ${\displaystyle AB}$, ako pripada toj duži i važi ${\displaystyle AS\cong SB}$

Teorema 4

Za svaku duž postoji jedinstveno središte.

Definicija 4

Duž AB je manja od duži CD u oznaci AB < CD ako unutar duži CD postoji tačka E takva da je AB ≅ CE. Takođe u tom slučaju se kaže i da je duž CD veća od duži AB u oznaci CD > AB.

Definicija 5

Duž EF jednaka je zbiru duži AB i CD u oznaci EF = AB + CD, ako unutar duži EF postoji tačka G takva da je AB≅EG CD ≅GF.

Na isti način definišu se razlika, proizvod duži i prirodnog broja, proizvod duži iracionalnog broja

Dva konveksna ili konkavna ugla ${\displaystyle pOq}$ i ${\displaystyle p_{1}O_{1}q_{1}}$ su podudarna ako i samo ako na kracima ${\displaystyle p}$ i ${\displaystyle q}$ ${\displaystyle p_{1}}$, ${\displaystyle q_{1}}$ redom postoje tačke ${\displaystyle P,Q,P_{1},Q_{1}}$ takve da je: ${\displaystyle (P,O,Q)\cong (P_{1},O_{1},Q_{1}}$).

Teorema 5

• Unakrsni uglovi su međusobno podudarni.
• Za svaki ∠pq i svaku polupravu p' neke ravni, postoji u poluravni određenoj pravom koja sadrži p', jedinstvena poluprava q' takva da ∠pq ≅ ∠p'q'.

Teorema 6

Svaki ugao ima jedinstvenu bisektrisu

Definicija 5

Ugao AOB je manji od ugla CSD u oznaci ${\displaystyle \angle AOB<\angle CSD}$ ako unutar ugla CSD postoji poluprava SE takva da je ${\displaystyle \angle AOB\cong \angle CSE}$. U tom slučaju kažemo ia je ugao CSD veći od ugla AOB u oznaci ${\displaystyle \angle CSD>\angle AOB}$.

Definicija 6

Uglom dve mimoilazne prave p i q u prostoru ${\displaystyle E^{3}}$ naziva se ugao koji određuju njima paralelene prave a i b koje se seku u nekoj tački O. Specijalno, ako je ugao dve mimoilazne prave u prostoru ${\displaystyle E^{3}}$ prav, tada se kaže da su prave ${\displaystyle p}$ i ${\displaystyle q}$ normalne među sobom, i simbolički označavamo sa ${\displaystyle p\perp q}$

Teorema 7

1. Ugao podudaran nekom pravom uglu takođe je prav.
2. Pravi uglovi su među sobom podudarni.
3. Postoji jedna i samo jedna prava koja seče svaku od dve mimoilazne prave a i b pod pravim uglom.

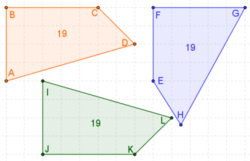
Dva podudarna poligona imaju isti broj stranica i vrhova.^[5]

Dva poligoni sa n strana su podudarna, ako i samo ako svaki od njih ima odgovarajuće stranice i uglove jednake.

1. Dva paralelograma su podudarna ako su im podudarne dve susedne ivice i jedan ugao.
2. Dva pravougaonika su podudarna ako su im podudarne dve susedne ivice.
3. Dva romba su podudarna ako su im podudarne jedna ivica i jedan ugao
4. Dva kvadrata su podudarna ako su im podudarne stranice.

Dva trougla su podudarna ako su njihove odgovarajuće stranice jednake dužine, odgovarajući uglovi jednake veličine. Da su dva trougla ABC i DEF podudarni zapisuje se

${\displaystyle \triangle \mathrm {ABC} \cong \triangle \mathrm {DEF} }$

• SUS

Dva trougla su podudarna ako su dve ivice i njima zahvaćeni ugao jednog trougla podudarni sa odgovarajućim ivicama i uglovima drugog trougla, tj: ${\displaystyle AB\cong A'B',AC\cong A'C',\angle BAC\cong \angle B'A'C'=>\triangle ABC\cong \triangle A'B'C'}$

• SSS

Dva trougla su podudarna ako su im odgovarajuće ivice podudarne, tj. ${\displaystyle AB\cong A'B',BC\cong B'C',AC\cong A'C'=>\triangle ABC\cong \triangle A'B'C'}$

Dokaz:

Neka su ABC, A'B'C' dva trougla takva da je ${\displaystyle AB\cong A'B',BC\cong B'C',AC\cong A'C'}$. Tada su i odgovarajući parovi tačaka podudarni tj. ${\displaystyle \triangle ABC\cong \triangle A'B'C'.}$

Postoji izometrija te ravni, koja tačke A,B,C preslikava redom u tačke A', B', C'. Izometrije čuvaju raspored, pa se odgovarajuće ivice jednog trougla preslikavaju u odgovarajuće ivice drugog trougla. Izometrija preslikava trougao ABC u trougao A'B'C', pa je ${\displaystyle \triangle ABC\cong \triangle A'B'C'.}$

• USU

Dva trougla su podudarna ako su jedna ivica i na njoj nalegli uglovi jednog trougla podudarni sa odgovarajućom ivicom i odgovarajućim uglovima drugog trougla, tj: ${\displaystyle BC\cong B'C',\angle ABC\cong \angle A'B'C',\angle ACB\cong \angle A'C'B'=>\triangle ABC\cong \triangle A'B'C'}$

• SSU

Dva trougla su podudarna ako su dve ivice i ugao naspram jedne od njih jednog trougla podudarni sa odgovarajućim stranicama i odgovarajućim uglom drugog trougla.^[6]