Fullständig fyrsiding

En fullständig fyrsiding. De fyra sidorna är heldragna, medan diagonalerna är prickade. De sex hörnen utgörs av punkterna A till F, medan de tre diagonalpunkterna är markerade med I, J och K.

En fullständig fyrsiding är en geometrisk figur bestående av fyra linjer ("sidor") som två och två skär varandra i sex olika punkter ("hörn").[1] Hörn som inte har någon gemensam sida kallas "motstående" och en linje genom två motstående hörn kallas "diagonal". Sammanlagt finns tre diagonaler och dessa skär varandra i tre "diagonalpunkter".
På varje diagonal finns således två hörn och två diagonalpunkter. Dessa ligger i ett harmoniskt delningsförhållande så att diagonalpunkterna är harmoniska konjugat till sträckan mellan hörnen och hörnen är harmoniska konjugat till sträckan mellan diagonalpunkterna.[2][3]
En fullständig fyrsiding kan användas för att konstruera en harmonisk delning endast med hjälp av linjal.[3]
Dualen till den fullständiga fyrsidingen, en fullständig fyrhörning, är en figur bestående av fyra punkter ("hörn") i vilka sammanlagt sex linjer ("sidor") skär varandra tre och tre.
Harmonisk delning
Att en diagonal delas harmoniskt av skärningspunkterna med de två andra diagonalerna samt de två hörn som diagonalen går genom visas nedan:
Betrakta triangeln i figur 1. De tre cevianerna , och skär varandra i punkten vilket enligt Cevas sats ger:
Betrakta linjen vilken skär sidorna på i punkterna , och . Menelaos sats ger oss att:
Division av 1 med 2 ger att dubbelförhållandet :
Det vill säga att punkterna , , och delar harmoniskt.
Betrakta nu linjeknippet (,,,) genom punkten , vilket delar harmoniskt. Men eftersom dubbelförhållanden och harmonisk delning är invarianta under centralprojektion följer att detta linjeknippe även delar diagonalen harmoniskt i punkterna , , och .
Linjeknippet (,,,) genom punkten delar också harmoniskt och således delas den tredje diagonalen, , harmoniskt av detta linjeknippe i punkterna , , och .
Konstruktion av den fjärde harmoniska delningspunkten enbart med hjälp av linjal eller rätskiva
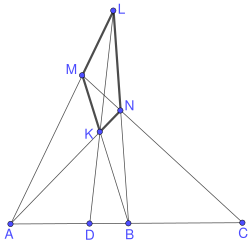
Notera att punkterna , , och , tillsammans med de sex linjerna genom dessa punkter bildar en fullständig fyrhörning. Man kan således även betrakta det som att man med hjälp av denna fullständiga fyrhörning kan dela linjen harmoniskt.
Givet: Två punkter och (se figur 3) samt antingen en inre delningspunkt (som inte får vara mittpunkt på sträckan eftersom den yttre delningspunkten då ligger i oändligheten) eller en yttre delningspunkt på den räta linjen genom och . Den givna delningspunkten får heller inte vara lika med eller .
Välj en godtycklig punkt (företrädesvis, men ej nödvändigtvis, så att dess fotpunkt på linjen genom och ligger mellan dessa båda punkter och närmare den av punkterna som ligger närmast den givna delningspunkten) och dra från denna räta linjer till och . Välj därefter den godtyckliga punkten på eller den godtyckliga punkten på
Om den inre delningspunkten är given:
Dra linjen och därfter antingen linjen eller linjen , beroende på om eller valts. vilket ger punkten på . Dra därefter den andra av eller genom . Linjen genom och ger då som skärningspunkt med linjen genom och .
Om den yttre delningspunkten är given:
Dra en linje från till , vilket ger oss , eller till vilket ger oss . Dra sedan linjerna och och kalla skärningspunkten mellan dessa för . Linjen skär då i den inre delningspunkten .
Att konstruktionen ger den fjärde delningspunkten framgår direkt ur förhållandet att linjerna , , och bildar en fullständig fyrsiding och att , och är diagonaler i denna.
Referenser
- ^ Christer Kiselman och Lars Mouwitz, 2008, Matematiktermer för skolan, sid. 207. Nationellt centrum för matematikutbildning, NCM, Göteborgs universitet. ISBN 978-91-85143-12-2
- ^ Harmonic ratio på Cut the Knot.
- ^ [a b] Lars-Åke Lindahl, 2004, En inledning till geometri, sid. 117.

















































