Pierwiastkowanie

Ten artykuł dotyczy odwrócenia potęgowania. Zobacz też: inne znaczenia słowa „pierwiastek”.

Pierwiastkowanie – operacja odwrotna względem potęgowania, zdefiniowana m. in. dla liczb rzeczywistych i zespolonych. Przy tym dla liczb rzeczywistych wprowadza się dwa pojęcia: pierwiastka arytmetycznego i pierwiastka algebraicznego.

Pierwiastki pojawiają się np. w definicji średniej geometrycznej, w pierwiastkowym kryterium Cauchy’ego na zbieżność szeregu liczbowego albo w definicji odległości Minkowskiego.

Pierwiastki zespolone z jedynki odgrywają istotną rolę w matematyce wyższej. Duża część teorii Galois skupia się na wskazaniu, które z liczb algebraicznych można przedstawić za pomocą pierwiastków, co prowadzi do twierdzenia Abela-Ruffiniego mówiącego, iż ogólny wielomian stopnia piątego bądź wyższego nie może być rozwiązany za pomocą tzw. pierwiastników, tzn. wyrażeń połączonych działaniami dodawania, odejmowania, mnożenia i dzielenia oraz pierwiastków.

Pierwiastek rzeczywisty arytmetyczny

Pierwiastki arytmetyczne definiuje się dla liczb rzeczywistych i w taki sposób, by przypisać liczbom rzeczywistym pierwiastki w sposób wzajemnie jednoznaczny, tj. każdej liczbie rzeczywistej odpowiada dokładnie jeden pierwiastek stopnia ${\displaystyle n}$-tego, przy czym nie istnieją pierwiastki arytmetyczne dla liczb ujemnych stopnia parzystego, np. pierwiastek drugiego stopnia z -1. Natomiast w dziedzinie liczb zespolonych pierwiastek ${\displaystyle n}$-tego stopnia z liczby -1 istnieje i ma ${\displaystyle n}$ wartości (por. dalej); w tym przypadku liczba -1 jest traktowana jako liczba zespolona o zerowej części urojonej. Także definiuje się tzw. pierwiastek algebraiczny w dziedzinie liczb rzeczywistych, który może mieć dwie wartości dla tej samej liczby.

Liczby rzeczywiste nieujemne

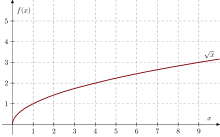
Pierwiastkiem arytmetycznym stopnia ${\displaystyle n=1,2,3,4\dots }$ z liczby rzeczywistej nieujemnej ${\displaystyle x\ (x\geq 0)}$ nazywamy taką liczbę rzeczywistą nieujemną ${\displaystyle y\ (y\geq 0)}$, która podniesiona do potęgi ${\displaystyle n}$ daje liczbę ${\displaystyle x}$, tj.

${\displaystyle y^{n}=x}$

i zapisuje się w postaci

${\displaystyle y={\sqrt[{n}]{x}}}$

W ten sposób każdej nieujemnej liczbie rzeczywistej przypisana zostaje jedna nieujemna liczba rzeczywista, będąca jej pierwiastkiem arytmetycznym.

Liczbę ${\displaystyle x}$ nazywamy liczbą podpierwiastkową.

Z definicji wynika, że pierwiastek stopnia ${\displaystyle n}$ z liczby ${\displaystyle x}$ jest pierwiastkiem równania ${\displaystyle y^{n}-x=0}$ zmiennej ${\displaystyle y}$ przy ustalonej wartości ${\displaystyle x}$.

Np. ${\displaystyle {\sqrt[{4}]{16}}=2}$ - pierwiastek arytmetyczny czwartego stopnia z ${\displaystyle 16}$, gdyż ${\displaystyle 2^{4}=16.}$

Uwaga: Jeżeli liczbę 16 będziemy traktować jako liczbę zespoloną (o zerowej części urojonej), to otrzymamy cztery pierwiastki ${\displaystyle {\sqrt[{4}]{16}}=2,-2,2i,-2i}$ (por. dalej - pierwiastki zespolone).

Liczby rzeczywiste ujemne i pierwiastek stopnia nieparzystego

Dla liczb rzeczywistych ujemnych ${\displaystyle x<0}$ pierwiastek stopnia nieparzystego ${\displaystyle n}$ definiuje się wzorem

${\displaystyle y=-{\sqrt[{n}]{|x|}}}$

gdzie ${\displaystyle |x|}$ - wartość bezwzględna liczby ${\displaystyle x}$

Np.${\displaystyle {\sqrt[{3}]{-8}}=-\ {\sqrt[{3}]{8}}=-2,\quad }$ ${\displaystyle {\sqrt[{5}]{-2}}=-\ {\sqrt[{5}]{2}}=-1{,}148698354\dots }$

Dla nieparzystych ${\displaystyle n}$ każda liczba rzeczywista ma w ten sposób zdefiniowany pierwiastek rzeczywisty n-tego stopnia.

Nie istnieje zaś rzeczywisty pierwiastek stopnia parzystego z liczby ujemnej, np. ${\displaystyle {\sqrt[{4}]{-8}}.}$ Jednak w dziedzinie liczb zespolonych ${\displaystyle {\sqrt[{4}]{-8}}}$ ma aż cztery różne wartości (por. dalej - pierwiastki zespolone).

Symbole pierwiastka arytmetycznego

Pierwiastki zapisuje się zwykle za pomocą symbolu ${\displaystyle {\sqrt {^{^{\;}}}}}$ (zob. niżej), pierwiastkom stopnia drugiego, trzeciego, czwartego itd. z liczby ${\displaystyle x}$ odpowiadają kolejno symbole ${\displaystyle {\sqrt {x}},{\sqrt[{3}]{x}},{\sqrt[{4}]{x}}}$ itp. (zwyczajowo pomija się w zapisie stopień pierwiastka kwadratowego). Notacja ta nie budzi zastrzeżeń w stosunku do pierwiastków arytmetycznych, niemniej może prowadzić do sprzeczności w przypadku pierwiastków algebraicznych, dla których symbole te nie są jednoznaczne, gdyż istnieje wiele pierwiastków algebraicznych danej liczby (por. niżej).

Pierwiastek kwadratowy, sześcienny i inne

Dla ${\displaystyle n=2}$ pierwiastek arytmetyczny nazywa się pierwiastkiem kwadratowym i oznacza ${\displaystyle {\sqrt {x}}}$,  pomijając cyfrę 2, zaś dla ${\displaystyle n=3}$ nazywa się pierwiastkiem sześciennym i oznacza ${\displaystyle {\sqrt[{3}]{x}}}$; pierwiastki wyższych stopni nazywa się wyłącznie liczbowo, np. „pierwiastek czwartego stopnia”.

Pierwiastkowanie to potęgowanie o ułamkowym wykładniku

Obliczanie pierwiastka ${\displaystyle n}$-tego stopnia jest operacją odwrotną do potęgowania, dlatego pierwiastkowanie można zapisywać jako potęgowanie o wykładniku ułamkowym, tj.

${\displaystyle {\sqrt[{n}]{x}}\equiv x^{1/n}.}$

Dowód:

Korzystając z twierdzenia o potędze ${\displaystyle (x^{a})^{b}=x^{a\cdot b}}$ potęgi mamy:

${\displaystyle (x^{1/n})^{n}=x^{{\frac {1}{n}}\cdot n}=x^{1}=x}$

Z drugiej strony, z definicji pierwiastka wynika, że ${\displaystyle n}$-ta potęga pierwiastka ${\displaystyle n}$-tego stopnia musi dać liczbę podpierwiastkową ${\displaystyle x,}$ tj.

${\displaystyle ({\sqrt[{n}]{x}})^{n}=x}$

Porównując obie równości dostajemy dowodzony wzór.

Twierdzenia - pierwiastki rzeczywiste

Jeżeli ${\displaystyle x,y}$ są nieujemnymi liczbami rzeczywistymi, zaś ${\displaystyle n,m}$ są dodatnimi liczbami całkowitymi, to:

• ${\displaystyle {\sqrt[{n}]{xy}}={\sqrt[{n}]{x}}{\sqrt[{n}]{y}}}$
• ${\displaystyle {\sqrt[{n}]{x/y}}={\frac {\sqrt[{n}]{x}}{\sqrt[{n}]{y}}}\quad {}}$ dla ${\displaystyle \ y\neq 0}$
• ${\displaystyle {\sqrt[{n}]{x^{m}}}=\left({\sqrt[{n}]{x}}\right)^{m}}$
• ${\displaystyle {\sqrt[{m}]{\sqrt[{n}]{x}}}={\sqrt[{m\cdot n}]{x}}}$

• gdy ${\displaystyle x<y}$ to ${\displaystyle {\sqrt[{n}]{x}}<{\sqrt[{n}]{y}}}$
• Pierwiastek kwadratowy z liczby naturalnej jest albo liczbą naturalną, albo niewymierną^[a]; np. dla liczby naturalnej 2:

${\displaystyle {\sqrt {2}}=1{,}414213562\dots }$

• Im większy stopień pierwiastka z liczby mniejszej od ${\displaystyle 1}$, tym większa jest jego wartość, która zmierza do 1 wraz ze wzrostem stopnia pierwiastka, np. ${\displaystyle {\sqrt[{2}]{0.4}}\approx 0{.}6<\quad {\sqrt[{5}]{0.4}}\approx 0{.}8<\quad {\sqrt[{100}]{0.4}}\approx 0{.}99}$
• Im większy stopień pierwiastka z liczby wiekszej od ${\displaystyle 1}$, tym mniejsza jest jego wartość, która zmierza do ${\displaystyle 1}$ wraz ze wzrostem stopnia pierwiastka, np. ${\displaystyle {\sqrt {2}}\approx 1{,}4>\quad {\sqrt[{3}]{2}}\approx 1{,}3>\quad {\sqrt[{100}]{2}}\approx 1{,}007}$

• Pierwiastki stopni całkowitych z liczb niewymiernych są niewymierne, bo liczba wymierna podniesiona do potęgi o dowolnym wykładniku całkowitym daje liczbę wymierną.

Pierwiastek rzeczywisty algebraiczny

Pierwiastkiem algebraicznym stopnia ${\displaystyle n}$ (gdzie ${\displaystyle n=1,2,\dots }$) z liczby rzeczywistej ${\displaystyle x}$ nazywamy taką liczbę rzeczywistą ${\displaystyle y}$ (dodatnią lub ujemną lub równą zero), która podniesiona do potęgi ${\displaystyle n}$ daje liczbę ${\displaystyle x}$^[1], tj.

${\displaystyle y^{n}=x}$

Pierwiastek algebraiczny z liczb rzeczywistych ujemnych stopnia parzystego nie istnieje, podobnie jak pierwiastek arytmetyczny stopnia parzystego, np. pierwiastek kwadratowy z ${\displaystyle -8}$. Ale istnieje pierwiastek algebraiczny dla dowolnych liczb rzeczywistych stopnia nieparzystego i ma zawsze jedną wartość, np. pierwiastek 3-go stopnia z ${\displaystyle -8}$ wynosi ${\displaystyle -2}$. Zaś dla liczb rzeczywistych dodatnich istnieją zawsze dwa pierwiastki algebraiczne stopnia parzystego. Np. dla liczby ${\displaystyle 4}$ istnieją dwie takie liczby: ${\displaystyle 2}$ oraz ${\displaystyle -2}$, gdyż ${\displaystyle 2^{2}=4}$ oraz ${\displaystyle (-2)^{2}=4}$ - obie te liczby nazywamy pierwiastkami kwadratowymi algebraicznymi z liczby ${\displaystyle 4}$.

Operacja znajdowania pierwiastka algebraicznego w dziedzinie liczb rzeczywistych przypisuje więc danej liczbie jedną wartość lub dwie wartości, inaczej niż dla pierwiastka arytmetycznego, który przyjmuje zawsze jedną wartość (oraz - tak jak w przypadku pierwiastka arytmetycznego - wyklucza przypisywanie pierwiastków stopnia parzystego liczbom ujemnym).

Pierwiastek zespolony

Df. Pierwiastkiem zespolonym stopnia ${\displaystyle n=1,2,3,4\dots }$ z liczby zespolonej ${\displaystyle z}$ nazywa się dowolną liczbę ${\displaystyle w}$ spełniającą równość

${\displaystyle w^{n}=z}$

Każda niezerowa liczba zespolona ${\displaystyle z}$ (w tym liczba rzeczywista, tj. zespolona o zerowej części urojonej) ma ${\displaystyle n}$ różnych zespolonych pierwiastków ${\displaystyle n}$-tego stopnia.

Tw. Aby wyznaczyć pierwiastki zespolone liczby zespolonej ${\displaystyle z=a+ib}$, przedstawia się ją w postaci trygonometrycznej:

${\displaystyle z=|z|\left(\cos \phi +i\sin \phi \right)}$

gdzie:

${\displaystyle |z|={\sqrt {a^{2}+b^{2}}}}$ - moduł

${\displaystyle \phi =\arctan(b/a)\in (-\pi ,\pi >}$ - argument główny

Wtedy pierwiastki ${\displaystyle n}$-go stopnia określa wzór de Moivre’a:

${\displaystyle w_{(k)}={\sqrt[{n}]{|z|}}\left(\cos {\tfrac {\phi +2k\pi }{n}}+i\sin {\tfrac {\phi +2k\pi }{n}}\right),}$

gdzie ${\displaystyle k=0,1,2,\dots ,n-1}$ oznacza numer pierwiastka (symbol ${\displaystyle {\sqrt[{n}]{\;}}}$ oznacza tu pierwiastek arytmetyczny).

Interpretacja geometryczna: W interpretacji geometycznej punkty przedstawiajace pierwiastki stopnia ${\displaystyle n}$ liczby zespolonej tworzą wierzchołki ${\displaystyle n}$-kata foremnego mającego środek w początku układu współrzędnych, wpisanego w okrąg o promieniu ${\displaystyle {\sqrt[{n}]{|z|}},}$ przy czym wektor wodzący wierzchołka o indeksie 0 jest pod katem ${\displaystyle \phi /n}$ do osi rzeczywistej układu współrzędnych. Ilustrują to przykłady.

Przykłady

Przykład 1: Pierwiastek kwadratowy z ${\displaystyle z=i}$

Niech będzie dana liczba czysto urojona ${\displaystyle z=i.}$ Liczba ta ma zerową część rzeczywistą, tj. ${\displaystyle z=0+1\cdot i}$ . Mamy więc moduł ${\displaystyle |z|=1}$, argument główny ${\displaystyle \phi =\pi /2}$, stąd postać trygonometryczna ${\displaystyle z=i=\cos {\tfrac {\pi }{2}}+i\sin {\tfrac {\pi }{2}}.}$

Z wzoru Moivre'a mamy pierwiastki 2-go stopnia z ${\displaystyle z=i}$

${\displaystyle w_{0}=\cos {\tfrac {\pi }{4}}+i\sin {\tfrac {\pi }{4}}={\tfrac {1}{\sqrt {2}}}+i{\tfrac {1}{\sqrt {2}}}}$

${\displaystyle w_{1}=\cos {\tfrac {3\pi }{2}}+i\sin {\tfrac {3\pi }{2}}=-{\tfrac {1}{\sqrt {2}}}-i{\tfrac {1}{\sqrt {2}}}}$

Pierwiastki te są leżą po przeciwnych stronach początku układu współrzędnych.

Przykład 2: Pierwiastki 2-go stopnia z -1

Niech będzie dana liczba ${\displaystyle z=-1.}$ W dziedzinie liczb rzeczywistych nie istnieje pierwiastek algebraiczny z liczby ujemnej stopnia parzystego. Jednak w dziedzinie liczb zespolonych liczba -1 jest liczbą o zerowej części urojonej i ma de facto postać ${\displaystyle z=-1+0\cdot i}$ . Mamy więc moduł ${\displaystyle |z|=1}$, argument główny ${\displaystyle \phi =\pi }$, stąd postać trygonometryczna ${\displaystyle z=-1=\cos \pi +i\sin \pi .}$

Z wzoru Moivre'a mamy pierwiastki 2-go stopnia z ${\displaystyle z=-1}$

${\displaystyle w_{0}=\cos {\tfrac {\pi }{2}}+i\sin {\tfrac {\pi }{2}}=i}$

${\displaystyle w_{1}=\cos {\tfrac {3\pi }{2}}+i\sin {\tfrac {3\pi }{2}}=-i}$

W dziedzinie zespolonej istnieją wiec dwa pierwiastki kwadratowe z ${\displaystyle z=-1:+i,-i.}$ (Każda liczba zespolona jest punktem na płaszczyźnie, w tym -1, sytuacja jest więc inna, niż w przypadku obliczania pierwiastków w dziedzinie rzeczywistej, gdzie liczby są punktami na prostej).

Przykład 3: Pierwiastki 3-go stopnia z -1

Aby obliczyć pierwiastki 3-go stopnia korzystamy z postaci trygonometrycznej ${\displaystyle z=-1=\cos \pi +i\sin \pi }$ oraz wzoru Moivre'a:

${\displaystyle w_{0}=\cos {\tfrac {\pi }{3}}+i\sin {\tfrac {\pi }{3}}={\tfrac {1}{2}}+i{\tfrac {\sqrt {3}}{2}}}$

${\displaystyle w_{1}=\cos {\tfrac {3\pi }{3}}+i\sin {\tfrac {3\pi }{3}}=-1}$

${\displaystyle w_{2}=\cos {\tfrac {4\pi }{3}}+i\sin {\tfrac {4\pi }{3}}={\tfrac {1}{2}}-i{\tfrac {\sqrt {3}}{2}}}$

Przykłady powyższe ilustrują ogólna prawidłowość, iż każda liczba zespolona ${\displaystyle z}$ ma ${\displaystyle n}$ pierwiastków ${\displaystyle n}$-tego stopnia - w tym liczby zespolone czysto rzeczywiste, które nie mają pierwiastków algebraicznych w dziedzinie liczb rzeczywistych.

Twierdzenia - pierwiastki zespolone. Subtelność funkcji wielowartościowych

W dziedzinie pierwiastków zespolonych obowiązują te same twierdzenia, co w dziedzinie liczb rzeczywistych, ale posługiwanie się nimi wymaga uwagi ze względu na wielowartościowość pierwiastków zespolonych. Np. zakładając słuszność twierdzenia ${\displaystyle {\sqrt[{n}]{z_{1}\cdot z_{2}}}\ ={\sqrt[{n}]{z}}_{1}{\sqrt[{n}]{z}}_{2}}$ otrzymamy

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {-1\cdot -1}}}$

Ale

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}=i\cdot i=i^{2}=-1}$

zaś

${\displaystyle {\sqrt {-1\cdot -1}}={\sqrt {1}}=1}$

- czyli sprzeczność. Sprzeczność wynika stąd, że w obliczeniach nie uwzględniono faktu, iż pierwiastki kwadratowe z liczb ${\displaystyle {\sqrt {-1}}}$ oraz ${\displaystyle {\sqrt {1}}}$ w dziedzinie liczb zespolonych mają po dwie wartości:

${\displaystyle {\sqrt {-1}}={\begin{cases}+i\\-i\end{cases}}\quad }$ oraz ${\displaystyle \quad {\sqrt {1}}={\begin{cases}+1\\-1\end{cases}}}$

Wtedy mamy:

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}={\begin{cases}i\cdot i=-1\\{\text{lub}}\\i\cdot (-i)=1\end{cases}}\quad }$

czyli dostajemy dwa wyniki, identyczne jak dla pierwiastka z 1.

Historia

Początki symbolu pierwiastka √ są dość niejasne. Niektóre źródła^{[potrzebny przypis]} podają, że symbol został wprowadzony przez Arabów, a po raz pierwszy został on użyty przez Abū al-Hasana ibn Alīego al-Qalasādīego (1421–1486) i został wyprowadzony z arabskiej litery ج, pierwszej litery słowa جذر (dżazr) oznaczającego „korzeń”. Wielu, w tym Leonhard Euler^[2] sądziło, że pochodzi on od litery r, pierwszej litery łacińskiego słowa radix (również oznaczającego „korzeń”), które oznacza to samo działanie matematyczne.

Nieużywany w języku polskim termin surd, traktowany niekiedy jako nazwa symbolu √^[3], pochodzi z czasów al-Khwārizmīego (ok. 825), który liczby wymierne i niewymierne nazywał odpowiednio „słyszalnymi” i „niesłyszalnymi”. W związku z tym arabskie assam („głuchy, głupi”) oznaczające liczbę niewymierną było później tłumaczone na łacinę jako surdus („głuchoniemy”). Gerard z Cremony (ok. 1150), Fibonacci (1202), a potem Robert Recorde (1551) używali tego terminu w odniesieniu do nierozwiązanych pierwiastków niewymiernych^[4].

Symbolu √ użyto po raz pierwszy w druku bez vinculum (poziomej kreski nad liczbami wewnątrz symbolu pierwiastka) w 1525 roku w Die Coss autorstwa niemieckiego matematyka Christoffa Rudolffa. Vinculum wprowadził Kartezjusz w Geometrii (1637) do zaznaczania, jakie wyrażenie algebraiczne podlega pierwiastkowaniu^[3].

Stosowana przez Kartezjusza notacja dla pierwiastków stopnia wyższego niż dwa nie przyjęła się (np. ${\displaystyle {\sqrt[{3}]{x}}}$ Kartezjusz zapisywał jako ${\displaystyle {\sqrt {C.x}}}$^[b])^[3]. Współczesną notację stopnia pierwiastka zaproponował Albert Girard w pracy z 1629 roku; utrwaliła się ona w pierwszej połowie XVIII w.^[5]

Typografia

Niżej przedstawiono kody znaków symboli pierwiastka. W notacji angielskiej znak pierwiastka występuje bez wiążącej kreski górnej^[6].

Znak	Nazwa polska[c]	Nazwa unikodowa	Unikod	Encja HTML			URL
				dec	hex	name
√	pierwiastek kwadratowy	SQUARE ROOT	U+221A	√	√	√	%E2%88%9A
∛	pierwiastek sześcienny	CUBE ROOT	U+221B	∛	∛	–	%E2%88%9B
∜	pierwiastek czwartego stopnia	FOURTH ROOT	U+221C	∜	∜	–	%E2%88%9C
‾	kreska wiążąca górna	OVERLINE	U+203E	‾	‾	‾	%E2%80%BE
‾	kreska wiążąca górna dostawna	COMBINING OVERLINE	U+0305	̅	̅	–	%00%CC%85

W LaTeX-u:

• pierwiastek ${\displaystyle {\sqrt {x}}}$ zapisywany jest jako \sqrt x;
• pierwiastek ${\displaystyle {\sqrt[{k}]{x}}}$ zapisywany jest jako \sqrt[k] x.

Zobacz też

Zobacz hasło pierwiastkowanie w Wikisłowniku

• pierwiastek kwadratowy
• pierwiastek sześcienny
• pierwiastki zespolone z jedynki
• wzór de Moivre'a
• algorytm Newtona numerycznego obliczania pierwiastka n-tego stopnia (dla liczby rzeczywistej)

Inne:

• Pomoc Wikipedii: Pierwiastki we wzorach matematycznych - nt. edycji wzorów za pomocą kodu

Uwagi

Bibliografia

• I. N. Bronsztejn, K. A. Siemiendiajew, Poradnik encyklopedyczny Matematyka, PWN, Warszawa 2019, str. 578-579.
• T. Trajdos, Matematyka dla inżynierów, PWN, Warszawa 1974, str. 412-416.

Przypisy